41. The state equation of a system is \[\mathop X\limits^ \cdot = \left[ {\begin{array}{*{20}{c}}
0&1\\
{ - 20}&9
\end{array}} \right]X + \left[ \begin{array}{l}
0\\
1
\end{array} \right]u\]
The poles of this system are located at:
The poles of this system are located at:
42. An automatic washing machine is
43. The initial slope of a type 2 system is
44. The system represented by the block diagram in the following figure is a hybrid servo system.
The components labelled 1, 2, 3 and 4 respectively
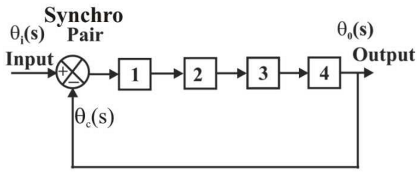
The components labelled 1, 2, 3 and 4 respectively

45. For good response of a second order control system-
1. higher tp (peak time) is needed
2. the maximum or peak overshoot must be less
3. The steady state error(ess) is less
4. The maximum or peak overshoot must be higher
Which of the above statements are correct?
1. higher tp (peak time) is needed
2. the maximum or peak overshoot must be less
3. The steady state error(ess) is less
4. The maximum or peak overshoot must be higher
Which of the above statements are correct?
46. Which of the following statements concerning the Bode plot are correct?
1. The relative stability can be obtained using Bode plots.
2. For a system with time delay, the phase plot does not reach a minimum value.
3. For a minimal system phase system, the phase plot reaches a minimum value.
4. Gain and phase margin can be used to ascertain the stability of a system using Bode plot.
1. The relative stability can be obtained using Bode plots.
2. For a system with time delay, the phase plot does not reach a minimum value.
3. For a minimal system phase system, the phase plot reaches a minimum value.
4. Gain and phase margin can be used to ascertain the stability of a system using Bode plot.
47. Consider the following systems:
Which of these systems can be modelled by the differential equation, $${a_2}\frac{{{d^2}y\left( t \right)}}{{d{t^2}}} + {a_1}\frac{{dy\left( t \right)}}{{dt}} + {a_0}y\left( t \right) = x\left( t \right)?$$
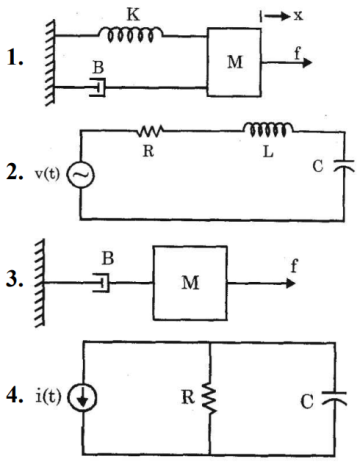
Which of these systems can be modelled by the differential equation, $${a_2}\frac{{{d^2}y\left( t \right)}}{{d{t^2}}} + {a_1}\frac{{dy\left( t \right)}}{{dt}} + {a_0}y\left( t \right) = x\left( t \right)?$$

48. For a unity feedback system with open-loop transfer function $$\frac{{25}}{{s\left( {s + 6} \right)}},$$ the resonant peak output Mm and the corresponding resonant frequency ωm are, respectively
49. The relative stability and the transient performance of a closed loop control system are directly related to location of
50. The output is said to be zero state response because . . . . . . . . conditions are made equal to zero.
Read More Section(Control Systems)
Each Section contains maximum 100 MCQs question on Control Systems. To get more questions visit other sections.
