51. Which of the following can work as error detecting devices?
1. A pair of potentiometers
2. A pair of synchros
3. A differential transformer
4. A Metadyne
5. A control transformer
1. A pair of potentiometers
2. A pair of synchros
3. A differential transformer
4. A Metadyne
5. A control transformer
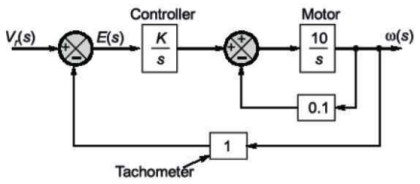
52. Consider the speed control system shown in the figure wherein the inner loop corresponds to motor back e.m.f, the controller is an integrator with gain K observes that the load is inertia only. What is the value of K for which steady-state error to unit ramp input $$\left( {{V_r}\left( s \right) = \frac{1}{{{s^2}}}} \right)$$ is less than 0.01 rad/sec?

53. The root locus of the system $$G\left( s \right)H\left( s \right) = \frac{K}{{s\left( {s + 2} \right)\left( {s + 3} \right)}},$$ has the break-away point located at
54. The closed loop transfer function of a control system is: $$\frac{K}{{s\left( {s + 1} \right)\left( {s + 5} \right) + K}}$$
What is the frequency of the sustained oscillations for marginally stable condition?
What is the frequency of the sustained oscillations for marginally stable condition?
55. Of the following transfer function second order linear time-invariant systems, the underdamped system is represented by
56. The current through a circuit element is $$\frac{{4{s^2}}}{{s + 7}}.$$ The current in t domain at t → ∞ and t → 0 will be respectively:
57. If a system is critically damped and gain is increased, the system
58. A second-order linear time-invariant system is described by the following state equations
\[\frac{{\rm{d}}}{{{\rm{dt}}}}\] x1(t) + 2x1(t) = 3u(t)
\[\frac{{\rm{d}}}{{{\rm{dt}}}}\] x2(t) + x2(t) = u(t)
where x1(t) and x2(t) are the two state variables and u(t) denotes the input. If the output c(t) = x1(t) , then the system is
\[\frac{{\rm{d}}}{{{\rm{dt}}}}\] x1(t) + 2x1(t) = 3u(t)
\[\frac{{\rm{d}}}{{{\rm{dt}}}}\] x2(t) + x2(t) = u(t)
where x1(t) and x2(t) are the two state variables and u(t) denotes the input. If the output c(t) = x1(t) , then the system is
59. In feedback control system with $$G\left( s \right) = \frac{{16}}{{s\left( {s + 4} \right)}}$$ and H(s) = 1 + Ks, the damping ratio of 0.6 will be achieved for K equal to
60. Which one of the following characteristic equation of result in the stable operation of the feedback system?
Read More Section(Control Systems)
Each Section contains maximum 100 MCQs question on Control Systems. To get more questions visit other sections.
