81. Two identical first order systems have been cascaded non-interactively, the unit step response of system is:
82. Match List-I with List-II and select the correct answer, using the options given below the lists:
List-I
List-II
a. Lag compensation
1. Exterior of unit Circle
b. Lead compensation
2. PD Control
c. Stability
3. Non-minimum phase
d. Instability
4. Left half of s-plane
5. PI control
| List-I | List-II |
| a. Lag compensation | 1. Exterior of unit Circle |
| b. Lead compensation | 2. PD Control |
| c. Stability | 3. Non-minimum phase |
| d. Instability | 4. Left half of s-plane |
| 5. PI control |
83. If a zero is added in a forward path of a second order system:
84. The phase margin of a system with the open-loop transfer function $$G\left( s \right)H\left( s \right) = \frac{{\left( {1 - s} \right)}}{{\left( {1 + s} \right)\left( {2 + s} \right)}}$$
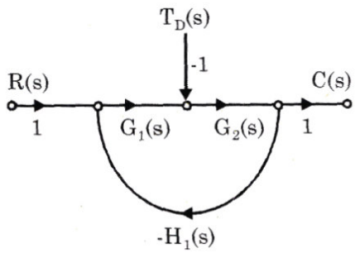
85. The signal flow graph of a closed-loop system is shown in the figure, where TD represents the disturbance in the forward path: The effect of the disturbance can be reduced by:

86. A unity feedback system has a forward path transfer function equal to $$\frac{{42.25}}{{s\left( {s + 6.5} \right)}}.$$ The unit step response of this system starting from rest, will have its maximum value at time equal to:
87. A second-order system has a transfer function given by $$G\left( s \right) = \frac{{25}}{{{s^2} + 8s + 25}}.$$ If the system, initially at rest, is subjected to a unit step input at t = 0. the second peak in the response will occur at
88. Given the state variable model {A, B, C} of a single-input, single-output system, the asymptotic stability is determined from:
89. The transfer function \[\frac{{Y\left( s \right)}}{{U\left( s \right)}}\] of a system described by the state equations \[\mathop {\rm{x}}\limits^ \cdot \](t) = -2x(t) + 2u(t) and y(t) = 0.5x(t) is
90. Consider the system \[\frac{{dx}}{{dt}} = Ax + Bu\] with \[A = \left[ {\begin{array}{*{20}{c}}
1&0\\
0&1
\end{array}} \right]\] and \[B = \left[ \begin{array}{l}
p\\
q
\end{array} \right]\] where p and q are arbitrary real numbers. Which of the following statements about the controllability of the system is true?
Read More Section(Control Systems)
Each Section contains maximum 100 MCQs question on Control Systems. To get more questions visit other sections.
