31. A periodic signal x(t) has a trigonometric Fourier series expansion
$$x\left( t \right) = {a_0} + \sum\limits_{n = 1}^\infty {\left( {{a_n}\,\cos \,n{\omega _0}t + {b_n}\sin \,n{\omega _0}t} \right)} $$
If $$x\left( t \right) = - x\left( { - t} \right) = - x\left( {{{t - \pi } \over {{\omega _0}}}} \right),$$ we can conclude that
$$x\left( t \right) = {a_0} + \sum\limits_{n = 1}^\infty {\left( {{a_n}\,\cos \,n{\omega _0}t + {b_n}\sin \,n{\omega _0}t} \right)} $$
If $$x\left( t \right) = - x\left( { - t} \right) = - x\left( {{{t - \pi } \over {{\omega _0}}}} \right),$$ we can conclude that
32. If $$F\left( s \right) = L\left| {f\left( t \right)} \right| = {K \over {\left( {s + 1} \right)\left( {{s^2} + 4} \right)}},$$ then $$\mathop {\lim }\limits_{t \to \infty } f\left( t \right)$$ is given by
33. The input to a channel is a bandpass signal. It is obtained by linearly modulating a sinusoidal carrier with a single-tone signal. The output of the channel due to this input is given by
$$y\left( t \right) = \left( {{1 \over {100}}} \right)\cos \left( {100t - {{10}^{ - 6}}} \right)\cos \left( {{{10}^6}t - 1.56} \right)$$
The group delay (tg) and the phase delay (tp) in seconds, of the channel are
$$y\left( t \right) = \left( {{1 \over {100}}} \right)\cos \left( {100t - {{10}^{ - 6}}} \right)\cos \left( {{{10}^6}t - 1.56} \right)$$
The group delay (tg) and the phase delay (tp) in seconds, of the channel are
34. Let x(t) be the input to a linear, time-invariant system. The required output is 4x(t - 2). The transfer function of the system should be
35. Let y[n] denote the convolution of h[n] and g[n], where h[n] = $${\left( {\frac{1}{2}} \right)^n}$$ u[n] and g[n] is a causal sequence. If y[0] = 1 and y[1] = $$\frac{1}{2},$$ then g[1] equals
36. The trigonometric Fourier series of an even function of time does not have
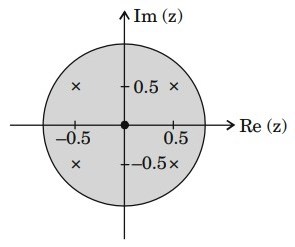
37. The pole-zero diagram of a causal and stable discrete-time system is shown in the figure. The zero at the origin has multiplicity 4. The impulse response of the system is h[n]. If h[0] = 1, we can conclude

38. Letx(t) be the input and y(t) be the output of a continuous time system. Match the system properties P1, P2 and P3 with system relations R1, R2, P3, P4.
Properties
P1 : Linear but NOT time-invariant
P2 : Time-invariant but NOT linear
P3 : Linear and time-invariant
Relations
R1 : y(t) = t2x(t)
R2 : y(t) = t |x(t)|
R3 : y(t) = |x(t)|
R4 : y(t) = x(t - 5)
Properties
P1 : Linear but NOT time-invariant
P2 : Time-invariant but NOT linear
P3 : Linear and time-invariant
Relations
R1 : y(t) = t2x(t)
R2 : y(t) = t |x(t)|
R3 : y(t) = |x(t)|
R4 : y(t) = x(t - 5)
39. The z-transform of the following real exponential sequence
x(nT) = an, nT ≥ 0
= 0, nT < 0, a > 0
x(nT) = an, nT ≥ 0
= 0, nT < 0, a > 0
40. Consider a single input single output discrete-time system with x[n] as input and y[n] as output, where the two are related as
$$y\left[ n \right] = \left\{ {\matrix{
{n\left| {x\left[ n \right]} \right|,} & {{\rm{for}}\,0 \le n \le 10} \cr
{x\left[ n \right] - x\left[ {n - 1} \right],} & {{\rm{otherwise}}} \cr
} } \right.$$
Which one of the following statements is true about the system?
$$y\left[ n \right] = \left\{ {\matrix{ {n\left| {x\left[ n \right]} \right|,} & {{\rm{for}}\,0 \le n \le 10} \cr {x\left[ n \right] - x\left[ {n - 1} \right],} & {{\rm{otherwise}}} \cr } } \right.$$
Which one of the following statements is true about the system?
Read More Section(Signal Processing)
Each Section contains maximum 100 MCQs question on Signal Processing. To get more questions visit other sections.
