41. Let the input be u and the output be y of a system, and the other parameters are real constants. Identify which among the following systems is not a linear system :
42. The z-transform of the time function $$\sum\limits_{k = 0}^\infty {\delta \left( {n - K} \right)} $$ is
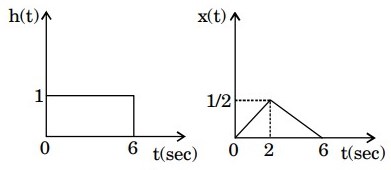
43. The impulse response and the excitation function of a linear time invariant causal system are shown in figure (a) and (b) respectively. The output of the system at t = 2 sec is equal to

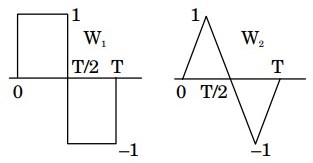
44. One period (0, T) each of two periodic waveforms W1 and W2 are shown in the figure. The magnitudes of the nth Fourier series coefficients of W1 and W2, for n ≥ 1, n is odd, are respectively proportional to

45. The Fourier Transform of the signal $$x\left( t \right) = {e^{ - 3{t^2}}}$$ is of the following form, where A and B are constants
46. The signal x(t) is described by
$$x\left( t \right) = \left\{ {\matrix{
{1\,{\rm{for}}} & { - 1 \le t \le + 1} \cr
{0,} & {{\rm{otherwise}}} \cr
} } \right.$$
Two of the angular frequencies at which its Fourier transform becomes zero are
$$x\left( t \right) = \left\{ {\matrix{ {1\,{\rm{for}}} & { - 1 \le t \le + 1} \cr {0,} & {{\rm{otherwise}}} \cr } } \right.$$
Two of the angular frequencies at which its Fourier transform becomes zero are
47. The trigonometric Fourier series of an even function does not have the
48. The impulse response of a system is h(t) = tu(t). For an input u(t - 1), the output is
49. The unit impulse response of a linear time invariant system is the unit step function u(t). For t > 0, the response of the system to an excitation e-at u(t), a > 0 will be
50. A signal x(n) = sin(ω0n + f) is the input to a linear time-invariant system having a frequency
response H(ejω). If ihe output of the system Ax(n - n0), then the most general form of ∠H(ejω) will be
Read More Section(Signal Processing)
Each Section contains maximum 100 MCQs question on Signal Processing. To get more questions visit other sections.
