71. A system which has a unique relationship between its input and output is called
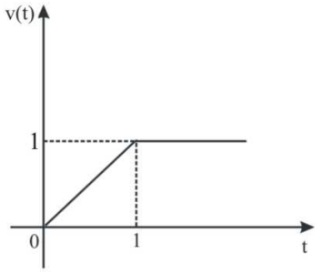
72. Laplace transform of the function v(t) shown in the figure is:

73. Let x(t) be the input and y(t) be the output of a continuous time system. Match the system properties P1, P2 and P3 with system relations R1, R2, R3, R4
Properties
P1: Linear but NOT time-invariant
P2: Time-invariant but NOT linear
P3: Linear and time-invariant
Relations
R1: y(t) = t2x(t)
R2: y(t)= t|x(t)|
R3: y(t) = |x(t)|
R4: y(t) = x(t - 5)
Properties
P1: Linear but NOT time-invariant
P2: Time-invariant but NOT linear
P3: Linear and time-invariant
Relations
R1: y(t) = t2x(t)
R2: y(t)= t|x(t)|
R3: y(t) = |x(t)|
R4: y(t) = x(t - 5)
74. A system whose impulse response is zero outside of some finite interval is termed as
75. For separating channels in FDM receivers
76. The probability cumulative distribution function must be monotone and
77. Given that x1(t) = ek1tu(t) and x2(t) = e-k2tu(t). Which one of the following gives their convolution?
78. What is the magnitude square function of a normalized Butterworth filter to 1 rad/sec cut-off frequency as
79. If F(s) and G(s) are the Laplace transform of f(t) and g(t), then their product F(s).G(s) = H(s), where H(s) is the Laplace transform of h(t), is defined as
80. Which one of the following statements is correct for the given system?
$$y\left( n \right) = {x^2}\left( n \right) + \frac{1}{{{x^2}\left( {n - 1} \right)}}$$
$$y\left( n \right) = {x^2}\left( n \right) + \frac{1}{{{x^2}\left( {n - 1} \right)}}$$
Read More Section(Signal Processing)
Each Section contains maximum 100 MCQs question on Signal Processing. To get more questions visit other sections.
