41. What is the value of the definite integral, $$\int\limits_0^{\text{a}} {\frac{{\sqrt {\text{x}} }}{{\sqrt {\text{x}} + \sqrt {{\text{a}} - {\text{x}}} }}} {\text{dx}}\,{\text{?}}$$
42. The direction of vector A is radially outward from the origin, with |A| = krn where r2 = x2 + y2 + z2 and k is a constant. The value of n for which $$\nabla \cdot {\text{A}} = 0$$ is
43. The angle of intersection of the curves x2 = 4y and y2 = 4x at point (0, 0) is
44. The expression e-$$l$$n x for x > 0 is equal to
45. While minimizing the function f(x), necessary and sufficient conditions for a point x0 to be a minima are
46. The function f(x) = x2 = x + x ...... x times, is defined
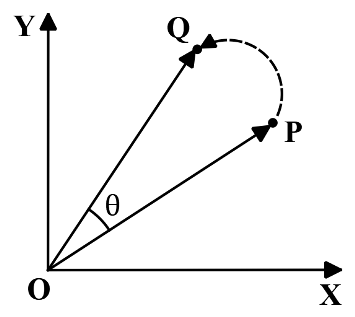
47. The position vector $$\overrightarrow {{\text{OP}}} $$ of P(20, 10) is rotated anti-clockwise in X-Y plane by an angle θ = 30° such that the point P occupies position Q, as shown in the figure. The coordinates (x, y) of Q are

48. If z = xy $$l$$n(xy), then
49. If $$\overrightarrow {\text{a}} $$ and $$\overrightarrow {\text{b}} $$ are two arbitrary vectors with magnitudes a and b, respectively, $${\left| {\overrightarrow {\text{a}} \times \overrightarrow {\text{b}} } \right|^2}$$ will be equal to
50. The value of the integral given below is
$$\int\limits_0^\pi {{{\text{x}}^2}\cos \,{\text{x dx}}} $$
$$\int\limits_0^\pi {{{\text{x}}^2}\cos \,{\text{x dx}}} $$
Read More Section(Calculus)
Each Section contains maximum 100 MCQs question on Calculus. To get more questions visit other sections.
