71. If \[{\text{f}}\left( {\text{x}} \right) = {\text{R}}\sin \left( {\frac{{\pi {\text{x}}}}{2}} \right) + {\text{S}},{\text{f}}'\left( {\frac{1}{2}} \right) = \sqrt 2 \] and \[\int\limits_0^1 {{\text{f}}\left( {\text{x}} \right){\text{dx}} = \frac{{2{\text{R}}}}{\pi }} ,\] then the constants R and S are, respectively
72. The vector function \[\overrightarrow {\text{A}} \] is given by \[\overrightarrow {\text{A}} = \overrightarrow \nabla {\text{u,}}\] where u(x, y) is a scalar function, Then \[\left| {\overrightarrow \nabla \times \overrightarrow {\text{A}} } \right|\]
73. If \[{\text{u}} = \log \left( {\frac{{{{\text{x}}^2} + {{\text{y}}^2}}}{{{\text{x}} + {\text{y}}}}} \right),\] what is the value of \[{\text{x}}\frac{{\partial {\text{u}}}}{{\partial {\text{x}}}} + {\text{y}}\frac{{\partial {\text{u}}}}{{\partial {\text{y}}}}\,?\]
74. Consider the plot f(x) versus x as shown below
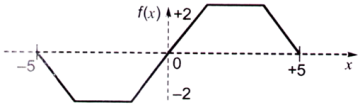
Suppose \[{\text{F}}\left( {\text{x}} \right) = \int_{ - 5}^x {{\text{f}}\left( {\text{y}} \right)} {\text{dy}}{\text{.}}\] Which one of the following is a graph of F(x)?

Suppose \[{\text{F}}\left( {\text{x}} \right) = \int_{ - 5}^x {{\text{f}}\left( {\text{y}} \right)} {\text{dy}}{\text{.}}\] Which one of the following is a graph of F(x)?
75. Consider the following definite integral:
\[{\text{I}} = \int\limits_0^1 {\frac{{{{\left( {{{\sin }^{ - 1}}{\text{x}}} \right)}^2}}}{{\sqrt {1 - {{\text{x}}^2}} }}{\text{dx}}} \]
The value of the integral is
\[{\text{I}} = \int\limits_0^1 {\frac{{{{\left( {{{\sin }^{ - 1}}{\text{x}}} \right)}^2}}}{{\sqrt {1 - {{\text{x}}^2}} }}{\text{dx}}} \]
The value of the integral is
76. The value of the directional derivative of the function \[\phi \](x, y, z) = xy2 + yz2 + zx2 at the point (2, -1, 1) in the direction of the vector p = i + 2j + 2k is
77. Which one of the following graphs describes the function f(x) = e-x(x2 + x + 1)?
78. \[\int\limits_0^{\frac{\pi }{4}} {\frac{{\left( {1 - \tan {\text{x}}} \right)}}{{\left( {1 + \tan {\text{x}}} \right)}}{\text{dx}}} \] evaluates to
79. Divergence of the three-dimensional radial vector field \[\overrightarrow {\text{r}} \] is
80. In the Taylor series expansion of exp(x) + sin(x) about the point x = π, the coefficient of (x - π)2 is
Read More Section(Calculus)
Each Section contains maximum 100 MCQs question on Calculus. To get more questions visit other sections.
