A particle of mass m is confined in an infinite potential well \[V\left( x \right) = \left\{ {\begin{array}{*{20}{c}} {0,}&{{\text{if }}0 < x < L} \\ {\infty ,}&{{\text{otherwise}}} \end{array}} \right.\]
It is subjected to a perturbing potential $${V_P}\left( x \right) = {V_0}\sin \left( {\frac{{2\pi x}}{L}} \right)$$     within the well. Let E⁽¹⁾ and E⁽²⁾ be the corrections to the ground state energy in the first and second order in V₀.

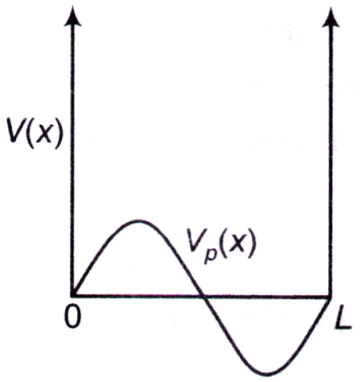
Which of the following is correct?

A particle is placed in a one-dimensional box of size L along the X-axis, (0 < x < L). Which of the following is true?

A. In the ground state, the probability of finding the particle in the interval $$\left( {\frac{L}{4},\,\frac{{3L}}{4}} \right)$$  is half

B. In the first excited state, the probability of finding the particle in the interval $$\left( {\frac{L}{4},\,\frac{{3L}}{4}} \right)$$  is half This also holds for states with n = 4, 6, 8, . . . .

C. For an arbitrary state $$\left| \psi \right\rangle ,$$  the probability of finding the particle in the left half of the well is half

D. In the ground state, the particle has a definite momentum

If the probability that x lies between x and x + dx is P(x) dx = ae^-ax dx, where 0 < x < $$\infty $$ , a > 0, then the probability that x lies between x₁ and x₂ (x₂ > x₁) is

A. (e^-ax₁ - e^-ax₂)

B. a(e^-ax₁ - e^-ax₂)

C. e^-ax₂ (e^-ax₁ - e^-ax₂)

D. None of the above

A Michelson interferometer is illuminated with monochromatic light. When one of the mirrors is moved through a distance of 25.3 μm, 92 fringes pass through the cross-wire. The wavelength of the monochromatic light is

A. 500 nm

B. 550 nm

C. 600 nm

D. 650 nm

An electron is in a statewith spin wavefunction \[{\phi _s} = \left[ {\begin{array}{*{20}{c}} {\frac{{\sqrt 3 }}{2}} \\ {\frac{1}{2}} \end{array}} \right]\]  in the s_z representation. What is the probability of, finding the z-component of its spin along the $$ - {\bf{\hat Z}}$$  direction?

A. 0.75

B. 0.50

C. 0.35

D. 0.25