A particle with energy E is in a time independent double well potential as shown in the figure. Which, of the following statements about the particle is not correct?
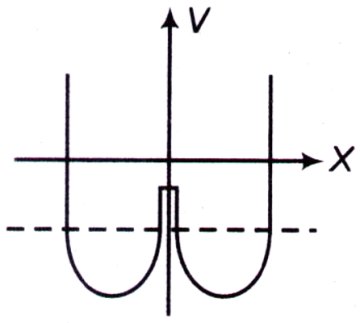
A. The particle will always be in a bound state
B. The probability of finding the particle in one well will be time dependent
C. The particle will be confined to anyone of the wells
D. The particle can tunnel from one well to the other and back
Answer: Option C
Join The Discussion
Comments (1)
A. In the ground state, the probability of finding the particle in the interval $$\left( {\frac{L}{4},\,\frac{{3L}}{4}} \right)$$ is half
B. In the first excited state, the probability of finding the particle in the interval $$\left( {\frac{L}{4},\,\frac{{3L}}{4}} \right)$$ is half This also holds for states with n = 4, 6, 8, . . . .
C. For an arbitrary state $$\left| \psi \right\rangle ,$$ the probability of finding the particle in the left half of the well is half
D. In the ground state, the particle has a definite momentum
A. (e-ax1 - e-ax2)
B. a(e-ax1 - e-ax2)
C. e-ax2 (e-ax1 - e-ax2)
D. None of the above

Can anyone explain why it is so