Communication Systems

A uniformly distributed random variable X with probability density function $${f_x}\left( x \right) = \frac{1}{{10}}\left( {u\left( {x + 5} \right) - u\left( {x - 5} \right)} \right)$$
Where u(⋅) is the unit step function is passed through a transformation given in the figure below. The probability density function of the transformed random variable Y would be

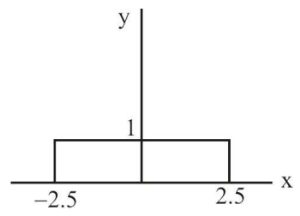
A) $${f_Y}\left( y \right) = \frac{1}{5}\left( {u\left( {y + 2.5} \right) - u\left( {y - 2.5} \right)} \right)$$ B) $${f_Y}\left( y \right) = 0.5\delta \left( y \right) + 0.5\delta \left( {y - 1} \right)$$ C) $${f_Y}\left( y \right) = 0.25\delta \left( {y + 2.5} \right) + 0.25\delta \left( {y - 2.5} \right) + 0.5\delta \left( y \right)$$ D) $${f_Y}\left( y \right) = 0.25\delta \left( {y + 2.5} \right) + 0.25\delta \left( {y - 2.5} \right) + \frac{1}{{10}}\left( {u\left( {y + 2.5} \right) - u\left( {y - 2.5} \right)} \right)$$

Answer & Solution

Correct Answer: Option B

Let's discuss the solution. Join the discussion

A uniformly distributed random variable X with probability density function f...

Join the Discussion

A uniformly distributed random variable X with probability density function f...

Join the Discussion

Related Questions on Communication Systems