Classical Mechanics MCQs Question and Answer in Engineering Physics

1

A mass m is constrained to move on a horizontal frictionless surface. It is set in circular motion with radius r₀ and angular speed ω₀ by an applied force $$\overrightarrow {\bf{F}} $$ communicated through an inextensible thread that passesthrough a hole on the surface as shown in figure given below. Then, this force is suddenly doubled.
Classical Mechanics mcq question image

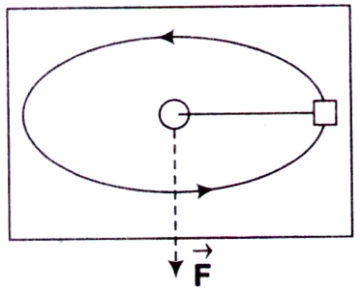
The magnitude of the radial velocity of the mass

A) increases till mass falls into hole B) decreases till mass falls into hole C) remains constant D) becomes zero at radius r₁, where 0 < r₁ < r₀

Discuss

Answer & Solution

Answer: Option D

No explanation is given for this question. Let's Discuss on Board

2

The speed of a particle whose kinetic energy is equal to its rest mass energy, is given by (c is the speed of light in vacuum)

A) $$\frac{c}{3}$$ B) $$\frac{{\sqrt 2 }}{3}c$$ C) $$\frac{c}{2}$$ D) $$\frac{{\sqrt 3 }}{2}c$$

Discuss

Answer & Solution

Answer: Option D

No explanation is given for this question. Let's Discuss on Board

3

The Hamiltonian corresponding to the Lagrangian $$L = a{{\dot x}^2} + b{{\dot y}^2} - kxy$$ is

A) $$\frac{{{p_x}^2}}{{2a}} + \frac{{{p_y}^2}}{{2b}} + kxy$$ B) $$\frac{{{p_x}^2}}{{4a}} + \frac{{{p_y}^2}}{{4b}} - kxy$$ C) $$\frac{{{p_x}^2}}{{4a}} + \frac{{{p_y}^2}}{{4b}} + kxy$$ D) $$\frac{{{p_x}^2 + {p_y}^2}}{{4ab}} + kxy$$

Discuss

Answer & Solution

Answer: Option C

No explanation is given for this question. Let's Discuss on Board

4

A particle is moving in an inverse square field. If the total energy of the particle is positive, then trajectory of particle is

A) circular B) elliptical C) parabolic D) hyperbolic

Discuss

Answer & Solution

Answer: Option C

No explanation is given for this question. Let's Discuss on Board

5

An object of mass m rests on a surface with coefficient of static friction μ. Which of the following is not correct?

A) The force of friction is exactly μmg B) The maximum force of friction is μmg C) The force of friction is along the surface D) The force of friction opposes any effort to move the object

Discuss

Answer & Solution

Answer: Option B

No explanation is given for this question. Let's Discuss on Board

6

Two solid spheres of radius R and mass M each are connected by a thin rigid rod of negligible mass. The distance between the centre is 4R. The moment of inertia about an axis passing through the centre of symmetry and perpendicular to the line joining the sphere is

A) $$\frac{{11}}{5}M{R^2}$$ B) $$\frac{{22}}{5}M{R^2}$$ C) $$\frac{{44}}{5}M{R^2}$$ D) $$\frac{{88}}{5}M{R^2}$$

Discuss

Answer & Solution

Answer: Option C

No explanation is given for this question. Let's Discuss on Board

7

A circular hoop of mass M and radius a rolls without slipping with constant angular speed ω along the horizontal X-axis in the X-Y plane. When the hoop is at a distance d = $$\sqrt 2 $$ a from the origin, the magnitude of the total angular momentum of the hoop about the origin is

A) Ma²ω B) $$\sqrt 2 $$ Ma²ω C) 2Ma²ω D) 3Ma²ω

Discuss

Answer & Solution

Answer: Option C

No explanation is given for this question. Let's Discuss on Board

8

Hamiltonian canonical equations of motion for a conservation system are

A) $$\frac{{ - d{q_i}}}{{dt}} = \frac{{\partial H}}{{\partial {P_i}}}{\text{ and }}\frac{{ - d{P_i}}}{{dt}} = \frac{{\partial H}}{{\partial {q_i}}}$$ B) $$\frac{{d{q_i}}}{{dt}} = \frac{{\partial H}}{{\partial {P_i}}}{\text{ and }}\frac{{d{P_i}}}{{dt}} = \frac{{\partial H}}{{\partial {q_i}}}$$ C) $$\frac{{ - d{q_i}}}{{dt}} = \frac{{\partial H}}{{\partial {P_i}}}{\text{ and }}\frac{{d{P_i}}}{{dt}} = \frac{{\partial H}}{{\partial {q_i}}}$$ D) $$\frac{{d{q_i}}}{{dt}} = \frac{{\partial H}}{{\partial {P_i}}}{\text{ and }}\frac{{ - d{P_i}}}{{dt}} = \frac{{\partial H}}{{\partial {q_i}}}$$

Discuss

Answer & Solution

Answer: Option D

No explanation is given for this question. Let's Discuss on Board

9

A cylinder of mass M and radius R is rolling down without slipping on an inclined plane of angle of inclination θ. The number of generalised coordinate required to describe the motion of the system is

A) 1 B) 2 C) 4 D) 6

Discuss

Answer & Solution

Answer: Option B

No explanation is given for this question. Let's Discuss on Board

10

A particle moves in a central force field $$\overrightarrow {\bf{F}} = k{r^n}{\bf{\hat r}},$$ where k is constant, r is distance of the particle from the origin and $${{\bf{\hat r}}}$$ is the unit vector in the direction of $$\overrightarrow {\bf{r}} $$. Closed stable orbits are possible for

A) n = 1 and n = 2 B) n = 1 and n = -1 C) n = 2 and n = -2 D) n = 1 and n = -2

Discuss

Answer & Solution

Answer: Option D

No explanation is given for this question. Let's Discuss on Board