For the given circuit, which one of the following is the correct state equation?

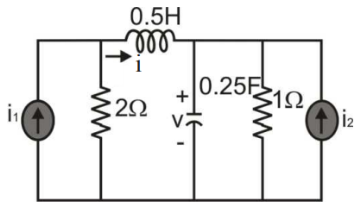
A. \[\frac{d}{{dt}}\left[ \begin{array}{l} v\\ i \end{array} \right] = \left[ {\begin{array}{*{20}{c}} { - 4}&4\\ { - 2}&{ - 4} \end{array}} \right]\left[ \begin{array}{l} v\\ i \end{array} \right] + \left[ {\begin{array}{*{20}{c}} 0&4\\ 4&0 \end{array}} \right]\left[ \begin{array}{l} {i_1}\\ {i_2} \end{array} \right]\]

B. \[\frac{d}{{dt}}\left[ \begin{array}{l} v\\ i \end{array} \right] = \left[ {\begin{array}{*{20}{c}} { - 4}&{ - 4}\\ { - 2}&{ - 4} \end{array}} \right]\left[ \begin{array}{l} v\\ i \end{array} \right] + \left[ {\begin{array}{*{20}{c}} 4&0\\ 0&4 \end{array}} \right]\left[ \begin{array}{l} {i_1}\\ {i_2} \end{array} \right]\]

C. \[\frac{d}{{dt}}\left[ \begin{array}{l} v\\ i \end{array} \right] = \left[ {\begin{array}{*{20}{c}} { - 4}&{ - 4}\\ { - 2}&4 \end{array}} \right]\left[ \begin{array}{l} v\\ i \end{array} \right] + \left[ {\begin{array}{*{20}{c}} 4&4\\ 4&0 \end{array}} \right]\left[ \begin{array}{l} {i_1}\\ {i_2} \end{array} \right]\]

D. \[\frac{d}{{dt}}\left[ \begin{array}{l} v\\ i \end{array} \right] = \left[ {\begin{array}{*{20}{c}} 4&{ - 4}\\ { - 2}&{ - 4} \end{array}} \right]\left[ \begin{array}{l} v\\ i \end{array} \right] + \left[ {\begin{array}{*{20}{c}} 0&4\\ 4&4 \end{array}} \right]\left[ \begin{array}{l} {i_1}\\ {i_2} \end{array} \right]\]

Answer: Option A