In the given figure, ABC is an equilateral triangle. Two circles of radius 4 cm and 12 cm are inscribed in the triangle. What is the side (in cm) of an equilateral triangle?

Solution (By Examveda Team)

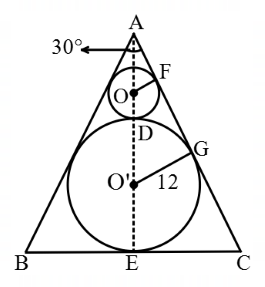
Now, In ΔAOF,
∠AFO = 90°
∠OAF = 30°

⇒ AF = $$4\sqrt 3 $$  cm
⇒ AO = 8 cm
and AE = AO + OD + DO' + O'E
= 8 + 4 + 12 + 12
= 36 cm
⇒ Median = 36 cm
In equilateral Δ,
$$\eqalign{ & {\text{Median}} = \frac{{\sqrt 3 }}{2} \times {\text{Side}} \cr & {\text{36}} = \frac{{\sqrt 3 }}{2} \times {\text{Side}} \cr & {\text{Side}} = \frac{{72}}{{\sqrt 3 }} \times \frac{{\sqrt 3 }}{{\sqrt 3 }} = 24\sqrt 3 {\text{ cm}} \cr} $$