The dependences of the magnetic susceptibility $$\left( \chi \right)$$ of a material with temperature (T) can be represented by $$\chi \propto \frac{1}{{T - \theta }},$$ where θ is the Curie-Weiss temperature. The plot of magnetic susceptibility versus temperature is sketched in the figure, as curves P, Q and R with curve Q having θ = 0. Which one of the following statements is correct?
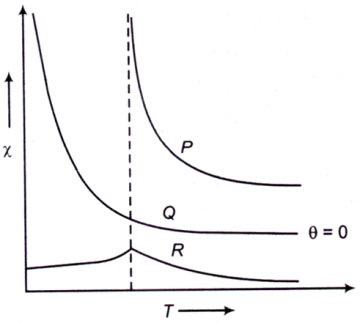
A. Curve R represents a paramagnet and Q a ferromagnetic field
B. Curve Q represents a ferromagnet and P an antiferromagnet
C. Curve R represents an antiferromagnet and Q a paramagnet
D. Curve R represents an antiferromagnet and Q a ferromagnet
Answer: Option C
The valence electrons do not directly determine the following property of a metal
A. electrical conductivity
B. thermal conductivity
C. shear modulus
D. metallic lustre
A. $${\left( {\frac{{2Q}}{P}} \right)^{ - 6}}$$
B. $${\left( {\frac{Q}{P}} \right)^{ - 6}}$$
C. $${\left( {\frac{P}{{2Q}}} \right)^{ - 6}}$$
D. $${\left( {\frac{P}{Q}} \right)^{ - 6}}$$
A. $$N\mu \coth \left( {\frac{{\mu B}}{{{k_B}T}}} \right)$$
B. $$N\mu \tanh \left( {\frac{{\mu B}}{{{k_B}T}}} \right)$$
C. $$N\mu \sinh \left( {\frac{{\mu B}}{{{k_B}T}}} \right)$$
D. $$N\mu \cosh \left( {\frac{{\mu B}}{{{k_B}T}}} \right)$$
A. $$\sqrt {2C\left( {\frac{1}{{{M_1}}} + \frac{1}{{{M_2}}}} \right)} $$
B. $$\sqrt {C\left( {\frac{1}{{2{M_1}}} + \frac{1}{{{M_2}}}} \right)} $$
C. $$\sqrt {C\left( {\frac{1}{{{M_1}}} + \frac{1}{{2{M_2}}}} \right)} $$
D. zero

Join The Discussion