The figure shows the plot of y as a function of x

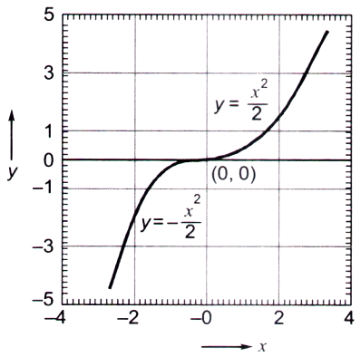
The function shown is the solution of the differential equation (assuming all initial conditions to be zero) is

The general solution of the differential equation, $$\frac{{{{\text{d}}^4}{\text{y}}}}{{{\text{d}}{{\text{x}}^4}}} - 2\frac{{{{\text{d}}^3}{\text{y}}}}{{{\text{d}}{{\text{x}}^3}}} + 2\frac{{{{\text{d}}^2}{\text{y}}}}{{{\text{d}}{{\text{x}}^2}}} - 2\frac{{{\text{dy}}}}{{{\text{dx}}}} + {\text{y}} = 0$$       is

A. $${\text{y}} = \left( {{{\text{C}}_1} - {{\text{C}}_2}{\text{x}}} \right){{\text{e}}^{\text{x}}} + {{\text{C}}_3}\cos {\text{x}} + {{\text{C}}_4}\sin {\text{x}}$$

B. $${\text{y}} = \left( {{{\text{C}}_1} + {{\text{C}}_2}{\text{x}}} \right){{\text{e}}^{\text{x}}} - {{\text{C}}_2}\cos {\text{x}} + {{\text{C}}_4}\sin {\text{x}}$$

C. $${\text{y}} = \left( {{{\text{C}}_1} + {{\text{C}}_2}{\text{x}}} \right){{\text{e}}^{\text{x}}} + {{\text{C}}_3}\cos {\text{x}} + {{\text{C}}_4}\sin {\text{x}}$$

D. $${\text{y}} = \left( {{{\text{C}}_1} + {{\text{C}}_2}{\text{x}}} \right){{\text{e}}^{\text{x}}} + {{\text{C}}_3}\cos {\text{x}} - {{\text{C}}_4}\sin {\text{x}}$$

The solution of the differential equation, $${\text{y}}\sqrt {1 - {{\text{x}}^2}} {\text{dy}} + {\text{x}}\sqrt {1 - {{\text{y}}^2}} {\text{dx}} = {\text{0}}$$      is

A. $$\sqrt {1 - {{\text{x}}^2}} = {\text{c}}$$

B. $$\sqrt {1 - {{\text{y}}^2}} = {\text{c}}$$

C. $$\sqrt {1 - {{\text{x}}^2}} + \sqrt {1 - {{\text{y}}^2}} = {\text{c}}$$

D. $$\sqrt {1 + {{\text{x}}^2}} + \sqrt {1 + {{\text{y}}^2}} = {\text{c}}$$

The maximum value of the solution y(t) of the differential equation \[{\rm{y}}\left( {\rm{t}} \right) + {\rm{\ddot y}}\left( {\rm{t}} \right) = 0\]    with initial conditions \[{\rm{\dot y}}\left( 0 \right) = 1\]  and y(0) = 1, for t ≥ 0 is

A. 1

B. 2

C. $$\pi $$

D. $$\sqrt 2 $$

The order of the differential equation $$\frac{{{{\text{d}}^2}{\text{y}}}}{{{\text{d}}{{\text{t}}^2}}} + {\left( {\frac{{{\text{dy}}}}{{{\text{dt}}}}} \right)^3} + {{\text{y}}^4} = {{\text{e}}^{ - {\text{t}}}}$$     is

A. 1

B. 2

C. 3

D. 4