The input voltage V1 and current I1 for linear passive network is given by V1 = AV2 - BI2 and I1 = CV2 - DI2
Now consider the following network:
Which one of the following is the transfer matrix \[\left[ {\begin{array}{*{20}{c}}
{\text{A}}&{\text{B}} \\
{\text{C}}&{\text{D}}
\end{array}} \right]\] of the network shown above?
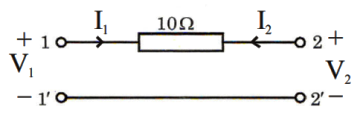
A. \[\left[ {\begin{array}{*{20}{c}} 1&0 \\ 0&{10} \end{array}} \right]\]
B. \[\left[ {\begin{array}{*{20}{c}} 1&{10} \\ 0&1 \end{array}} \right]\]
C. \[\left[ {\begin{array}{*{20}{c}} 0&1 \\ {10}&0 \end{array}} \right]\]
D. \[\left[ {\begin{array}{*{20}{c}} 0&{10} \\ 1&0 \end{array}} \right]\]
Answer: Option B
This Question Belongs to Electronics And Communications Engineering >> Network Theory And Analysis
Join The Discussion