A particle of mass m is moving in a potential of the form V(x, y, z) = $$\frac{1}{2}$$ mω2 (3x2 + 3y2 + 2z2 + 2xy). The oscillation frequencies of the three normal modes of the particle are given by
A. ω, $$\sqrt 3 $$ ω and $$\sqrt 3 $$ ω
B. $$\sqrt 2 $$ ω, $$\sqrt 3 $$ ω and $$\sqrt 3 $$ ω
C. $$\sqrt 2 $$ ω, $$\sqrt 2 $$ ω and 2ω
D. $$\sqrt 2 $$ ω, 2ω and 2ω
Answer: Option A
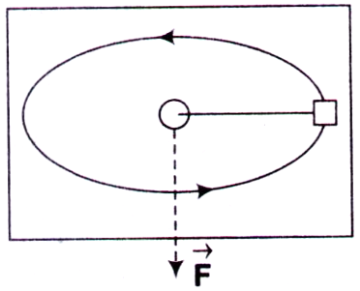
A. increases till mass falls into hole
B. decreases till mass falls into hole
C. remains constant
D. becomes zero at radius r1, where 0 < r1 < r0
A. $$\frac{c}{3}$$
B. $$\frac{{\sqrt 2 }}{3}c$$
C. $$\frac{c}{2}$$
D. $$\frac{{\sqrt 3 }}{2}c$$
The Hamiltonian corresponding to the Lagrangian $$L = a{{\dot x}^2} + b{{\dot y}^2} - kxy$$ is
A. $$\frac{{{p_x}^2}}{{2a}} + \frac{{{p_y}^2}}{{2b}} + kxy$$
B. $$\frac{{{p_x}^2}}{{4a}} + \frac{{{p_y}^2}}{{4b}} - kxy$$
C. $$\frac{{{p_x}^2}}{{4a}} + \frac{{{p_y}^2}}{{4b}} + kxy$$
D. $$\frac{{{p_x}^2 + {p_y}^2}}{{4ab}} + kxy$$
A. circular
B. elliptical
C. parabolic
D. hyperbolic

Join The Discussion