A rod of length L0 makes an angle θ0 with the Y-axis in its rest frame while the rest frame moves to the right along the X-axis with relativistic speed v with respect to lab frame. If $$\gamma = {\left( {1 - \frac{{{v^2}}}{{{c^2}}}} \right)^{ - \frac{1}{2}}},$$ the angle in the lab frame is
A. $$\theta = {\tan ^{ - 1}}\left( {\gamma \tan {\theta _0}} \right)$$
B. $$\theta = {\tan ^{ - 1}}\left( {\gamma \cot {\theta _0}} \right)$$
C. $$\theta = {\tan ^{ - 1}}\left( {\frac{{\tan {\theta _0}}}{\gamma }} \right)$$
D. $$\theta = {\tan ^{ - 1}}\left( {\frac{{\cot {\theta _0}}}{\gamma }} \right)$$
Answer: Option B
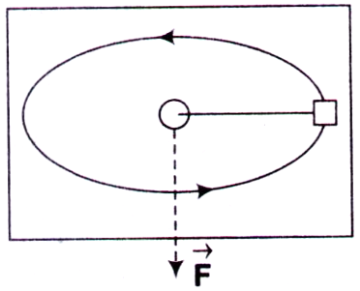
A. increases till mass falls into hole
B. decreases till mass falls into hole
C. remains constant
D. becomes zero at radius r1, where 0 < r1 < r0
A. $$\frac{c}{3}$$
B. $$\frac{{\sqrt 2 }}{3}c$$
C. $$\frac{c}{2}$$
D. $$\frac{{\sqrt 3 }}{2}c$$
The Hamiltonian corresponding to the Lagrangian $$L = a{{\dot x}^2} + b{{\dot y}^2} - kxy$$ is
A. $$\frac{{{p_x}^2}}{{2a}} + \frac{{{p_y}^2}}{{2b}} + kxy$$
B. $$\frac{{{p_x}^2}}{{4a}} + \frac{{{p_y}^2}}{{4b}} - kxy$$
C. $$\frac{{{p_x}^2}}{{4a}} + \frac{{{p_y}^2}}{{4b}} + kxy$$
D. $$\frac{{{p_x}^2 + {p_y}^2}}{{4ab}} + kxy$$
A. circular
B. elliptical
C. parabolic
D. hyperbolic

Join The Discussion