A simply supported beam with a gradually varying load from zero at ‘B’ and ‘w’ per unit length at ‘A’ is shown in the below figure. The shear force at ‘B’ is equal to
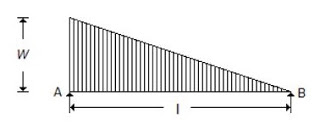
A. $$\frac{{{\text{w}}l}}{6}$$
B. $$\frac{{{\text{w}}l}}{3}$$
C. $${\text{w}}l$$
D. $$\frac{{2{\text{w}}l}}{3}$$
Answer: Option A
Solution (By Examveda Team)
This Question Belongs to Mechanical Engineering >> Strength Of Materials In ME
Join The Discussion
Comments (5)
Related Questions on Strength of Materials in ME
A. Equal to
B. Less than
C. Greater than
D. None of these
A. $$\frac{{{\text{w}}l}}{6}$$
B. $$\frac{{{\text{w}}l}}{3}$$
C. $${\text{w}}l$$
D. $$\frac{{2{\text{w}}l}}{3}$$
The columns whose slenderness ratio is less than 80, are known as
A. Short columns
B. Long columns
C. Weak columns
D. Medium columns
Takr Sum of all force in y direction = 0
We get , Ra + Rb = WL / 2
Where WL / 2 is load due to UVL
Then take sum of moment @ A = 0
Then we get ,
WL^2/ 6 - Rb L = 0
Rb = WL /6
Resolve the distributed loads into point load by using the formula (1/2*b*h) ,that will give u "wl/2" and it would be L/3 from A(base) and 2L/3 from B(apex) .Get the reacting component at point A by taking the moment about point B,that will give you "wl/3",then get the share force at be by taking ∑fy=0,that will be wl/2-wl/3=wl/6.
Wl/3
Convert the UVL into a Point Load by calculating the area of the triangular loading. i.e. (1/2)*L*W.
The load will act at CG of the triangle i.e. at L/3 from support A.
Now to calculate the reaction at B, take summation of the moment at A equal to zero(Equilibrium equation).
i can't understand. please described it.