A water tap fills a tub in 'p' hours and a sink at the bottom empties it in 'q' hours. If p < q and both tap and sink are opened the tank is filled in 'r' hours, then the relation between p, q, r :

A. $$\frac{1}{r} = \frac{1}{p} + \frac{1}{q}$$

B. $$\frac{1}{r} = \frac{1}{p} - \frac{1}{q}$$

C. $$r{\text{ = }}p{\text{ }} + {\text{ }}q$$

D. $${\text{ }}r{\text{ }} = {\text{ }}p{\text{ }} - {\text{ }}q$$

Answer: Option B

Solution(By Examveda Team)

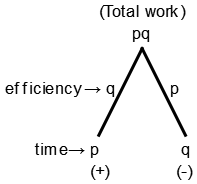
Net efficiency = q - p (∵ q > p)
Time required
$$\eqalign{ & {\text{r}} = \frac{{pq}}{{q - p}} \cr & or\,\frac{1}{r} = \frac{1}{p} - \frac{1}{q} \cr} $$