According to Euler's column theory, the crippling load for a column length $$l$$ hinged at both ends, is
A. $$\frac{{{\pi ^2}{\text{E}}I}}{{{l^2}}}$$
B. $$\frac{{{\pi ^2}{\text{E}}I}}{{4{l^2}}}$$
C. $$\frac{{4{\pi ^2}{\text{E}}I}}{{{l^2}}}$$
D. $$\frac{{2{\pi ^2}{\text{E}}I}}{{{l^2}}}$$
Answer: Option A
This Question Belongs to Mechanical Engineering >> Strength Of Materials In ME
Join The Discussion
Comments ( 1 )
Related Questions on Strength of Materials in ME
A. Equal to
B. Less than
C. Greater than
D. None of these
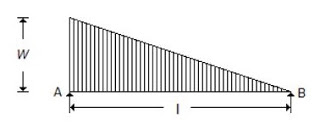
A. $$\frac{{{\text{w}}l}}{6}$$
B. $$\frac{{{\text{w}}l}}{3}$$
C. $${\text{w}}l$$
D. $$\frac{{2{\text{w}}l}}{3}$$
The columns whose slenderness ratio is less than 80, are known as
A. Short columns
B. Long columns
C. Weak columns
D. Medium columns
Both end fixed L = l/2 and Load = pi^2 * E * I/((l/2)^2),
Both end Hinged L = l and Load = pi^2 * E * I/(l^2),
one Fixed another Hinged L = l/Root 2,
one end fixed another free L = 2 * l.