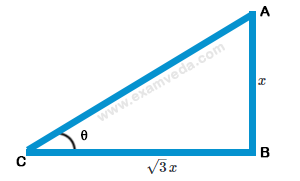
41. The length of shadow of a tower on the plane ground is $$\sqrt 3 $$ times the height of the tower. The angle of elevation of sun is
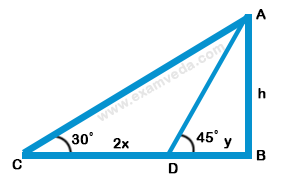
42. The length of the shadow of a tower standing on level ground is found to 2x meter longer when the sun’s elevation is 30° than when it was 45 °. The height of the tower in meters is
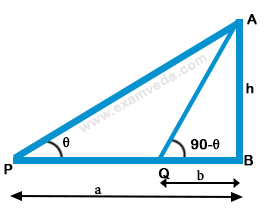
43. If the angle of elevation of the top of a tower from two points distant a and b from the base and in the same straight line with It are complementary, then the height of the tower is
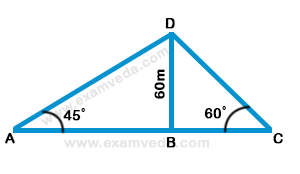
44. The angle of elevation of the top of a lighthouse 60 m high, from two points on the ground on its opposite sides are 45° and 60°. What is the distance between these two points?
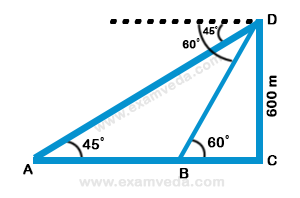
45. On the same side of a tower, two objects are located. Observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 600 m, the distance between the objects is approximately equal to :
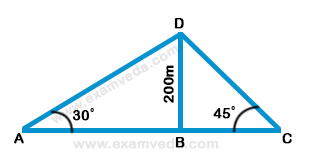
46. Two ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse is observed from the ships are 30º and 45º respectively. If the lighthouse is 200 m high, the distance between the two ships is:
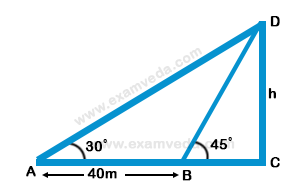
47. The angle of elevation of the top of a tower from a certain point is 30°. If the observer moves 40 m towards the tower, the angle of elevation of the top of the tower increases by 15°. The height of the tower is:
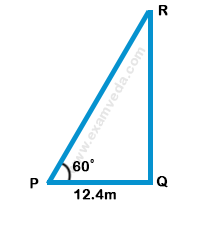
48. The angle of elevation of a ladder leaning against a wall is 60º and the foot of the ladder is 12.4 m away from the wall. The length of the ladder is:
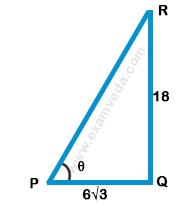
49. Find the angle of elevation of the sun when the shadow of a pole of 18 m height is $$6\sqrt 3 $$ m long?
50. A balloon leaves the earth at a point A and rises vertically at uniform speed. At the end of 2 minutes, John finds the angular elevation of the balloon as 60°. If the point at which John is standing is 150 m away from point A, what is the speed of the balloon?
Read More Section(Height and Distance)
Each Section contains maximum 100 MCQs question on Height and Distance. To get more questions visit other sections.