Consider a system whose input x and output y are related by the equation
$$y\left( t \right) = \int\limits_{ - \infty }^\infty {x\left( {t - \tau } \right)h\left( {2\tau } \right)d\tau } $$
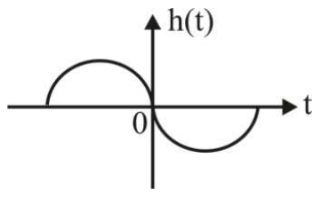
where h(t) is shown in the graph
Which of the following four properties are possessed by the system?
BIBO: Bounded input gives a bounded output
Causal : The system is causal
LP : The system is low pass
LTI : The system is linear and time-invariant
A. Causal, LP
B. BIBO, LTI
C. BIBO, Causal, LTI
D. LP, LTI
Answer: Option B
This Question Belongs to Electronics And Communications Engineering >> Signal Processing
Related Questions on Signal Processing
The Fourier transform of a real valued time signal has
A. Odd symmetry
B. Even symmetry
C. Conjugate symmetry
D. No symmetry
A. $$V$$
B. $${{{T_1} - {T_2}} \over T}V$$
C. $${V \over {\sqrt 2 }}$$
D. $${{{T_1}} \over {{T_2}}}V$$
A. $$T = \sqrt 2 {T_s}$$
B. T = 1.2Ts
C. Always
D. Never
A. $${{\alpha - \beta } \over {\alpha + \beta }}$$
B. $${{\alpha \beta } \over {\alpha + \beta }}$$
C. α
D. β
Join The Discussion