1. The Fourier transform of a real valued time signal has
2. The RMS value of a rectangular wave of period T, having a value of +V for a duration, T1(< T) and -V for the duration, T - T1 = T2 equals
3. A continuous time function x(t) is periodic with period T. The function is sampled uniformly with a sampling period Ts. In which one of the following cases is the sampled signal periodic?
4. The phase response of a passband waveform at the receiver is given by
$$\varphi \left( f \right) = - 2\pi \alpha \left( {f - {f_c}} \right) - 2\alpha \beta {f_c},$$
where fc is the centre frequency, and α and β are positive constants. The actual signal propagation delay from the transmittance to receiver is
$$\varphi \left( f \right) = - 2\pi \alpha \left( {f - {f_c}} \right) - 2\alpha \beta {f_c},$$
where fc is the centre frequency, and α and β are positive constants. The actual signal propagation delay from the transmittance to receiver is
5. For a given sample-and-hold circuit, if the value of the hold capacitor is increased, then
6. A continuous time LTI system is described by
$${{{d^2}y\left( t \right)} \over {d{t^2}}} + 4{{dy\left( t \right)} \over {dt}} + 3y\left( t \right) = 2{{dx\left( t \right)} \over {dt}} + 4x\left( t \right)$$
Assuming zero initial conditions, the response y(t) of the above system for the input x(t) = e-2tu(t) is given by
$${{{d^2}y\left( t \right)} \over {d{t^2}}} + 4{{dy\left( t \right)} \over {dt}} + 3y\left( t \right) = 2{{dx\left( t \right)} \over {dt}} + 4x\left( t \right)$$
Assuming zero initial conditions, the response y(t) of the above system for the input x(t) = e-2tu(t) is given by
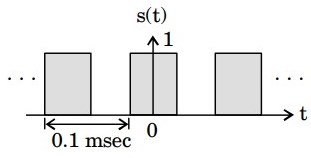
7. A rectangular pulse train s(t) as shown in the figure is convolved with the signal cos2(4π × 103t). The convolved signal will be a

8. The transfer function of a zero-order hold is
9. The 3-dB bandwidth of the low-pass signal e-tu(t), where u(t) is the unit step function, is given by
10. A system is described by the differential equation $${{{d^2}y} \over {d{t^2}}} + 5{{dy} \over {dt}} + 6y\left( t \right) = x\left( t \right).$$ Let x(t) be a rectangular pulse given by
$$x\left( t \right) = \left\{ {\matrix{
{1,} & {0 < t < 2} \cr
{0,} & {{\rm{otherwise}}} \cr
} } \right.$$
Assuming that y(0) = 0 and $${{dy} \over {dt}} = 0$$ at t = 0, the Laplace transform of y(t) is
$$x\left( t \right) = \left\{ {\matrix{ {1,} & {0 < t < 2} \cr {0,} & {{\rm{otherwise}}} \cr } } \right.$$
Assuming that y(0) = 0 and $${{dy} \over {dt}} = 0$$ at t = 0, the Laplace transform of y(t) is
Read More Section(Signal Processing)
Each Section contains maximum 100 MCQs question on Signal Processing. To get more questions visit other sections.
