51. The system represented by the state variable model \[\mathop X\limits^. = \left[ {\begin{array}{*{20}{c}}
0&{ - 1}\\
1&{ - 2}
\end{array}} \right]X + \left[ \begin{array}{l}
1\\
2
\end{array} \right]U\] is:
52. Consider unity feedback system with forward path transfer function $$\frac{{25}}{{s\left( {s + 5} \right)}};$$ what are the values of peak time and settling time?
53. A system with gain margin close to unity or a phase margin close to zero is:
54. Consider the state space system expressed by the signal flow diagram in the figure.
The corresponding system is
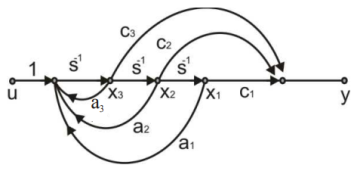
The corresponding system is

55. The loop transfer function of an LTI system is $$G\left( s \right)H\left( s \right) = \frac{{K\left( {s + 1} \right)\left( {s + 5} \right)}}{{s\left( {s + 2} \right)\left( {s + 3} \right)}}.$$ For K > 0, the point on the real axis final DOES NOT belong to the root locus of the system is
56. A plant transfer function is given as $$G\left( s \right) = \left( {{K_P} + \frac{{{K_I}}}{s}} \right)\left( {\frac{1}{{s\left( {s + 2} \right)}}} \right).$$ When the plant operates in a unity feedback configuration, the condition for the stability of the closed loop system is
57. When all the roots of characteristic equation are found in the left half of s-plane, the system response due to initial condition will:
58. The polar diagram of conditionally stable system for open loop gain k = 1 is shown in the figure. The open loop transfer function of the system is known to be stable. The closed loop system is stable for
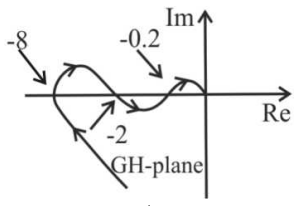

59. The open loop transfer function of a system is $$G\left( s \right)H\left( s \right) = \frac{K}{{\left( {1 + s} \right)\left( {1 + 2s} \right)\left( {1 + 3s} \right)}}$$
The phase crossover frequency ωpc is:
The phase crossover frequency ωpc is:
60. The most commonly used input signal (s) in control system is/are
Read More Section(Control Systems)
Each Section contains maximum 100 MCQs question on Control Systems. To get more questions visit other sections.
