1. The state model
\[\begin{array}{l}
x\left( {k + 1} \right) = \left[ {\begin{array}{*{20}{c}}
0&1\\
{ - \beta }&{ - \alpha }
\end{array}} \right]x\left( k \right) + \left[ \begin{array}{l}
0\\
1
\end{array} \right]u\left( k \right)\\
y\left( k \right) = \left[ {0\,\,\,1} \right]\left[ {\begin{array}{*{20}{c}}
{{x_1}}&{\left( k \right)}\\
{{x_2}}&{\left( k \right)}
\end{array}} \right]
\end{array}\]
is represented in the difference equation as
\[\begin{array}{l} x\left( {k + 1} \right) = \left[ {\begin{array}{*{20}{c}} 0&1\\ { - \beta }&{ - \alpha } \end{array}} \right]x\left( k \right) + \left[ \begin{array}{l} 0\\ 1 \end{array} \right]u\left( k \right)\\ y\left( k \right) = \left[ {0\,\,\,1} \right]\left[ {\begin{array}{*{20}{c}} {{x_1}}&{\left( k \right)}\\ {{x_2}}&{\left( k \right)} \end{array}} \right] \end{array}\]
is represented in the difference equation as
2. The state equation of a second-order linear system is given by, \[\mathop x\limits^ \cdot \left( t \right) = Ax\left( t \right),\,x\left( 0 \right) = {x_0}\]
For \[{x_0} = \left[ \begin{array}{l}
1\\
- 1
\end{array} \right],\,x\left( t \right) = \left[ \begin{array}{l}
{e^{ - t}}\\
- {e^{ - t}}
\end{array} \right]\] and for \[{x_0} = \left[ \begin{array}{l}
0\\
1
\end{array} \right],\,x\left( t \right) = \left[ \begin{array}{l}
{e^{ - t}} - {e^{ - 2t}}\\
- {e^{ - t}} + {e^{ - 2t}}
\end{array} \right].\]
When \[{x_0} = \left[ \begin{array}{l}
3\\
5
\end{array} \right],\,x\left( t \right)\] is
For \[{x_0} = \left[ \begin{array}{l} 1\\ - 1 \end{array} \right],\,x\left( t \right) = \left[ \begin{array}{l} {e^{ - t}}\\ - {e^{ - t}} \end{array} \right]\] and for \[{x_0} = \left[ \begin{array}{l} 0\\ 1 \end{array} \right],\,x\left( t \right) = \left[ \begin{array}{l} {e^{ - t}} - {e^{ - 2t}}\\ - {e^{ - t}} + {e^{ - 2t}} \end{array} \right].\]
When \[{x_0} = \left[ \begin{array}{l} 3\\ 5 \end{array} \right],\,x\left( t \right)\] is
3. By adding zero to the system transfer function, the improvement to transient response is called as:
4. Settling time is the time required for the system response to settle within a certain percentage of:
5. In position control system, the device used for providing rate feedback voltage is called-
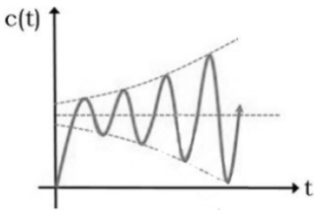
6. The given figure represents:

7. Consider the following statements:
The effect of phase lead network is given as:
1. Increased velocity constant.
2. Increased phase margin.
3. Increased bandwidth.
4. Slower response.
Which of the above statements are correct?
The effect of phase lead network is given as:
1. Increased velocity constant.
2. Increased phase margin.
3. Increased bandwidth.
4. Slower response.
Which of the above statements are correct?
8. The transfer function of a phase lead controller is $$\frac{{1 + 3Ts}}{{1 + Ts}}.$$ The maximum value of phase provided by this controller is
9. The transfer function of a first-order process is given by $$\frac{{Y\left( s \right)}}{{R\left( s \right)}} = G\left( s \right) = \frac{K}{{\tau s + 1}}$$
Then the impulse response to an impulse strength of 5 is
Then the impulse response to an impulse strength of 5 is
Read More Section(Control Systems)
Each Section contains maximum 100 MCQs question on Control Systems. To get more questions visit other sections.
