1. The transfer function of a discrete time LTI system is given by$$H\left( z \right) = \frac{{2 - \frac{3}{4}{z^{ - 1}}}}{{1 - \frac{3}{4}{z^{ - 1}} + \frac{1}{8}{z^{ - 2}}}}$$
Consider the following statements:
S1 : The system is stable and causal for $${\text{ROC}}:\left| z \right| > \frac{1}{2}$$
S2 : The system is stable but not causal for $${\text{ROC}}:\left| z \right| < \frac{1}{4}$$
S3 : The system is neither stable nor causal for $${\text{ROC}}:\frac{1}{4} < \left| z \right| < \frac{1}{2}$$
Which one of the following statements is valid?
Consider the following statements:
S1 : The system is stable and causal for $${\text{ROC}}:\left| z \right| > \frac{1}{2}$$
S2 : The system is stable but not causal for $${\text{ROC}}:\left| z \right| < \frac{1}{4}$$
S3 : The system is neither stable nor causal for $${\text{ROC}}:\frac{1}{4} < \left| z \right| < \frac{1}{2}$$
Which one of the following statements is valid?
2. The approximate transition width of main lobe in Blackman window is
3. Consider the two different ways of cascading a decimator with an interpolator shown below
The two systems are identical if-
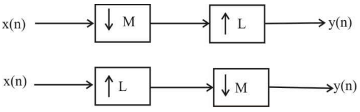
The two systems are identical if-

4. A signal xn, is given by x0 = 3, x1 = 2, x2 = 5, x3 = 1, x4 = 0, x5 = 1, x6 = 2, x7 = 2, x8 = 4, where the subscript 'n' denotes time. The peak value of the auto correlation of x2n - 11 is
5. The Causal system given by H(z) = 6 + z-1 - z-2 is
6. What is the Nyquist rate for the signal x(t) = cos2000πt + 3sin6000πt ?
7. What is the minimum sampling rate required to avoid aliasing for the signal $$m\left( t \right) = {\left( {\frac{{\sin \left( {2\pi t} \right)}}{{2\pi t}}} \right)^3}$$
8. The continuous time unit-step function is defined by
9. Match List-I with List-II and select the correct answer using the options given below:
List-I
List-II
a. $${\alpha ^n}u\left( n \right)$$
1. $$\frac{{\alpha {z^{ - 1}}}}{{{{\left( {1 - \alpha {z^{ - 1}}} \right)}^2}}}{\text{ROC}}:\left| z \right| > \left| \alpha \right|$$
b. $$ - {\alpha ^n}u\left( { - n - 1} \right)$$
2. $$\frac{1}{{\left( {1 - \alpha {z^{ - 1}}} \right)}}{\text{ROC}}:\left| z \right| > \left| \alpha \right|$$
c. $$ - n{\alpha ^n}u\left( { - n - 1} \right)$$
3. $$\frac{1}{{\left( {1 - \alpha {z^{ - 1}}} \right)}}{\text{ROC}}:\left| z \right| < \left| \alpha \right|$$
d. $$n{\alpha ^n}u\left( n \right)$$
4. $$\frac{{\alpha {z^{ - 1}}}}{{{{\left( {1 - \alpha {z^{ - 1}}} \right)}^2}}}{\text{ROC}}:\left| z \right| < \left| \alpha \right|$$
| List-I | List-II |
| a. $${\alpha ^n}u\left( n \right)$$ | 1. $$\frac{{\alpha {z^{ - 1}}}}{{{{\left( {1 - \alpha {z^{ - 1}}} \right)}^2}}}{\text{ROC}}:\left| z \right| > \left| \alpha \right|$$ |
| b. $$ - {\alpha ^n}u\left( { - n - 1} \right)$$ | 2. $$\frac{1}{{\left( {1 - \alpha {z^{ - 1}}} \right)}}{\text{ROC}}:\left| z \right| > \left| \alpha \right|$$ |
| c. $$ - n{\alpha ^n}u\left( { - n - 1} \right)$$ | 3. $$\frac{1}{{\left( {1 - \alpha {z^{ - 1}}} \right)}}{\text{ROC}}:\left| z \right| < \left| \alpha \right|$$ |
| d. $$n{\alpha ^n}u\left( n \right)$$ | 4. $$\frac{{\alpha {z^{ - 1}}}}{{{{\left( {1 - \alpha {z^{ - 1}}} \right)}^2}}}{\text{ROC}}:\left| z \right| < \left| \alpha \right|$$ |
10. The positions of the poles for the Butterworth filter lie on . . . . . . . . and the positions of the poles for the Chebyshev filter lie on . . . . . . . .
Read More Section(Signal Processing)
Each Section contains maximum 100 MCQs question on Signal Processing. To get more questions visit other sections.
