1. What is the value of \[\mathop {\mathop {\lim }\limits_{{\text{x}} \to 0} }\limits_{{\text{y}} \to 0} \frac{{{\text{xy}}}}{{{{\text{x}}^2} + {{\text{y}}^2}}}?\]
2. The Taylor series expansion of 3 sinx + 2 cosx is . . . . . . . .
3. \[\mathop {\lim }\limits_{{\text{x}} \to \infty } \sqrt {{{\text{x}}^2} + {\text{x}} - 1} - {\text{x is}}\]
4. The Taylor series expansion of \[\frac{{\sin {\text{x}}}}{{{\text{x}} - \pi }}\] at \[{\text{x}} = \pi \] is given by
5. If x = a (θ + sin θ) and y = a (1 - cos θ), then \[\frac{{{\text{dy}}}}{{{\text{dx}}}}\] will be equal to
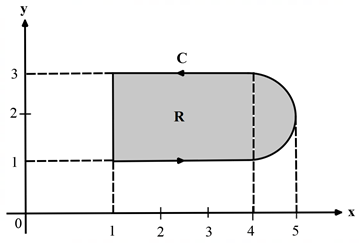
6. Consider the line integral \[\int\limits_{\text{C}} {\left( {{\text{xdy}} - {\text{ydx}}} \right)} \] the integral being taken in a counterclockwise direction over the closed curve C that forms the boundary of the region R shown in the figure below. The region R is the area enclosed by the union of a 2 × 3 rectangle and a semi-circle of radius 1. The line integral evaluates to

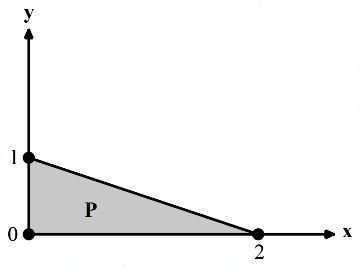
7. Consider the shaded triangular region P shown in the figure. What is If $$\iint\limits_{\text{P}} {{\text{xydxdy}}\,?}$$

8. Let \[\phi \] be an arbitrary smooth real valued scalar function and V be an arbitrary smooth vector valued function in a three-dimensional space. Which one of the following is an identity?
9. The magnitude of the directional derivative of the function f(x, y) = x2 + 3y2 in a direction normal to the circle x2 + y2 = 2, at the point (1, 1), is
10. If $${\text{S}} = \int\limits_1^\infty {{{\text{x}}^{ - 3}}{\text{dx,}}} $$ then S has the value
Read More Section(Calculus)
Each Section contains maximum 100 MCQs question on Calculus. To get more questions visit other sections.
