41. For a small value of h, the Taylor series expansion for f(x + h) is
42. The divergence of the vector field \[{\rm{3xz\hat i}} + 2{\rm{xy\hat j}} - {\rm{y}}{{\rm{z}}^2}{\rm{\hat k}}\] at a point (1, 1, 1) is equal to
43. The right circular cone of largest volume that can be enclosed by a sphere of 1 m radius has a height of
44. The area enclosed between the curves y2 = 4x and x2 = 4y is
45. It is known that two roots of the nonlinear equation x3 - 6x2 + 11x - 6 = are 1 and 3. The third root will be
46. The derivative of f(x) = cos x can be estimated using the approximation \[{\text{f}}'\left( {\text{x}} \right) = \frac{{{\text{f}}\left( {{\text{x}} + {\text{h}}} \right) - {\text{f}}\left( {{\text{x}} - {\text{h}}} \right)}}{{2{\text{h}}}}.\]
The percentage error is calculated as \[\left( {\frac{{{\text{Exact value}} - {\text{Approx value}}}}{{{\text{Exact value}}}} \times 100} \right)\]
The percentage error in the derivative of f(x) at \[{\text{x}} = \frac{\pi }{6}\] radian choosing h = 0.1 radian is
The percentage error is calculated as \[\left( {\frac{{{\text{Exact value}} - {\text{Approx value}}}}{{{\text{Exact value}}}} \times 100} \right)\]
The percentage error in the derivative of f(x) at \[{\text{x}} = \frac{\pi }{6}\] radian choosing h = 0.1 radian is
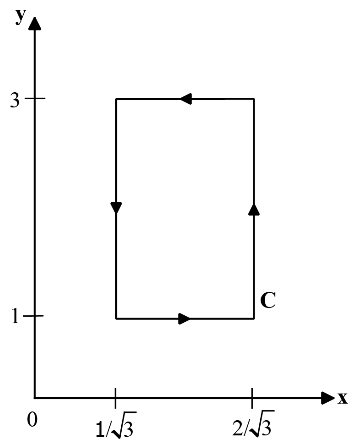
47. If \[\overrightarrow {\rm{A}} = {\rm{xy}}{{{\rm{\hat a}}}_{\rm{x}}} + {{\rm{x}}^2}{{{\rm{\hat a}}}_{\rm{y}}},\,\oint\limits_{\rm{c}} {\overrightarrow {\rm{A}} \cdot {\rm{d}}\overrightarrow l } \] over the path shown in the figure is

48. The expression \[\mathop {\lim }\limits_{\alpha \to 0} \frac{{{{\text{x}}^\alpha } - 1}}{\alpha }\] is equal to
49. It is known that two roots of the non-linear equation x3 - 6x2 + 11x - 6 = 0 and 1 and 3. The third root will be
50. Consider the function y = x2 - 6x + 9. The maximum value of y obtained when x varies over the interval 2 to 5 is
Read More Section(Calculus)
Each Section contains maximum 100 MCQs question on Calculus. To get more questions visit other sections.
