1. f(z) = u(x, y) + iv(x, y) is an analytic function or complex variable z = x + iy where $${\text{i}} = \sqrt { - 1} ,$$ u(x, y) = 2xy, then v(x, y) may be expressed as
2. The product of complex numbers (3 - 2i) and (3 + i4) results in
3. If a complex number $${\text{z}} = \frac{{\sqrt 3 }}{2} + {\text{i}}\frac{1}{2}$$ then z4 is
4. If C is a circle of radius r with centre z0, in the complex z-plane and if n is a non-zero integer, then $$\oint {\frac{{{\text{dz}}}}{{{{\left( {{\text{z}} - {{\text{z}}_0}} \right)}^{{\text{n}} + 1}}}}} $$ equals
5. Contour C in the adjoining figure is described by x2 + y2 = 16. The value $$\oint\limits_{\text{c}} {\frac{{{{\text{z}}^2} + 8}}{{0.5{\text{z}} - 1.5{\text{j}}}}{\text{dz}}} $$ is (Note: $${\text{j}} = \sqrt { - 1} $$ )
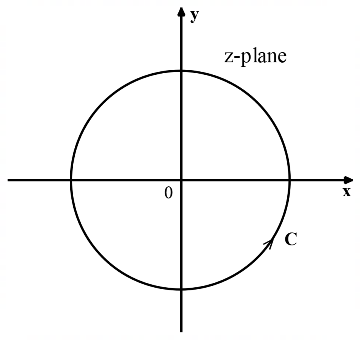
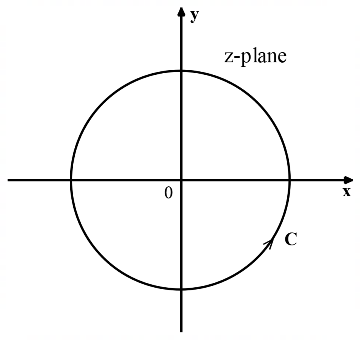
6. The value of $$\oint {\frac{{\sin {\text{z}}}}{{\text{z}}}{\text{dz,}}} $$ where the counter of integration is a simple closed curve around the origin, is
7. $${\text{z}} = \frac{{2 - 3{\text{j}}}}{{ - 5 + {\text{i}}}}$$ can be expressed as
8. Consider the following complex function $${\text{f}}\left( {\text{z}} \right) = \frac{9}{{\left( {{\text{z}} - 1} \right){{\left( {{\text{z}} + 2} \right)}^2}}}$$
Which of the following is one of the residues of the above function?
Which of the following is one of the residues of the above function?
