If $$\cos \theta = \frac{{2p}}{{1 + {p^2}}},$$ then tanθ is equal to:
A. $$\frac{{{p^2}}}{{1 + {p^2}}}$$
B. $$\frac{{2p}}{{1 + {p^2}}}$$
C. $$\frac{{1 - {p^2}}}{{1 + {p^2}}}$$
D. $$\frac{{1 - {p^2}}}{{2p}}$$
Answer: Option D
Solution (By Examveda Team)
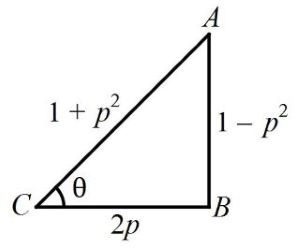
$$\eqalign{ & \cos \theta = \frac{{2p}}{{1 + {p^2}}} \cr & A{B^2} = {\left( {1 + {p^2}} \right)^2} - {\left( {2p} \right)^2} \cr & AB = 1 - {p^2} \cr & \tan \theta = \frac{{1 - {p^2}}}{{2p}} \cr} $$
This Question Belongs to Arithmetic Ability >> Trigonometry
Join The Discussion