If for a system of N particles of different masses m1, m2, . . . mN with position vectors $${\overrightarrow {\bf{r}} _1},\,{\overrightarrow {\bf{r}} _2},\,.\,.\,.\,{\overrightarrow {\bf{r}} _N}$$ and corresponding velocities $${\overrightarrow {\bf{v}} _1},\,{\overrightarrow {\bf{v}} _2},\,.\,.\,.\,{\overrightarrow {\bf{v}} _N}$$ respectively such that $$\sum\limits_i {\overrightarrow {{{\bf{v}}_i}} = 0,} $$ then
A. total momentum must be zero
B. total angular momentum must be independent of the choice of the origin
C. the total force on the system must be zero
D. the total torque on the system must be zero
Answer: Option C
This Question Belongs to Engineering Physics >> Classical Mechanics
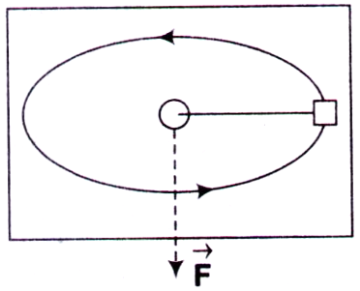
A. increases till mass falls into hole
B. decreases till mass falls into hole
C. remains constant
D. becomes zero at radius r1, where 0 < r1 < r0
A. $$\frac{c}{3}$$
B. $$\frac{{\sqrt 2 }}{3}c$$
C. $$\frac{c}{2}$$
D. $$\frac{{\sqrt 3 }}{2}c$$
The Hamiltonian corresponding to the Lagrangian $$L = a{{\dot x}^2} + b{{\dot y}^2} - kxy$$ is
A. $$\frac{{{p_x}^2}}{{2a}} + \frac{{{p_y}^2}}{{2b}} + kxy$$
B. $$\frac{{{p_x}^2}}{{4a}} + \frac{{{p_y}^2}}{{4b}} - kxy$$
C. $$\frac{{{p_x}^2}}{{4a}} + \frac{{{p_y}^2}}{{4b}} + kxy$$
D. $$\frac{{{p_x}^2 + {p_y}^2}}{{4ab}} + kxy$$
A. circular
B. elliptical
C. parabolic
D. hyperbolic
Join The Discussion