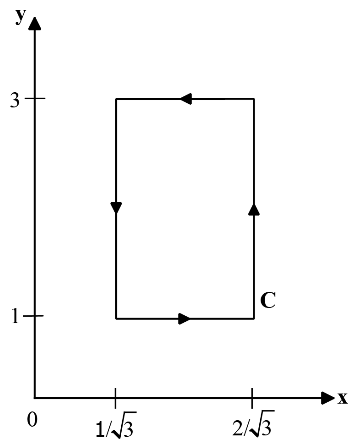
If \[\overrightarrow {\rm{A}} = {\rm{xy}}{{{\rm{\hat a}}}_{\rm{x}}} + {{\rm{x}}^2}{{{\rm{\hat a}}}_{\rm{y}}},\,\oint\limits_{\rm{c}} {\overrightarrow {\rm{A}} \cdot {\rm{d}}\overrightarrow l } \]     over the path shown in the figure is

What is the value of \[\mathop {\mathop {\lim }\limits_{{\text{x}} \to 0} }\limits_{{\text{y}} \to 0} \frac{{{\text{xy}}}}{{{{\text{x}}^2} + {{\text{y}}^2}}}?\]

A. 1

B. -1

D. Limit does not exit

The Taylor series expansion of 3 sinx + 2 cosx is . . . . . . . .

A. 2 + 3x - x² - \[\frac{{{{\text{x}}^3}}}{2}\] + ...

B. 2 - 3x + x² - \[\frac{{{{\text{x}}^3}}}{2}\] + ...

C. 2 + 3x + x² + \[\frac{{{{\text{x}}^3}}}{2}\] + ...

D. 2 - 3x - x² + \[\frac{{{{\text{x}}^3}}}{2}\] + ...

\[\mathop {\lim }\limits_{{\text{x}} \to \infty } \sqrt {{{\text{x}}^2} + {\text{x}} - 1} - {\text{x is}}\]

B. \[\infty \]

C. \[\frac{1}{2}\]

D. \[ - \infty \]

The Taylor series expansion of \[\frac{{\sin {\text{x}}}}{{{\text{x}} - \pi }}\]  at \[{\text{x}} = \pi \]  is given by

A. \[1 + \frac{{{{\left( {{\text{x}} - \pi } \right)}^2}}}{{3!}} + ...\]

B. \[ - 1 - \frac{{{{\left( {{\text{x}} - \pi } \right)}^2}}}{{3!}} + ...\]

C. \[1 - \frac{{{{\left( {{\text{x}} - \pi } \right)}^2}}}{{3!}} + ...\]

D. \[ - 1 + \frac{{{{\left( {{\text{x}} - \pi } \right)}^2}}}{{3!}} + ...\]