The figure shows a shape ABC and its mirror image A1B1C1 across the horizontal axis (X-axis). The coordinate transformation matrix that maps ABC to A1B1C1 is
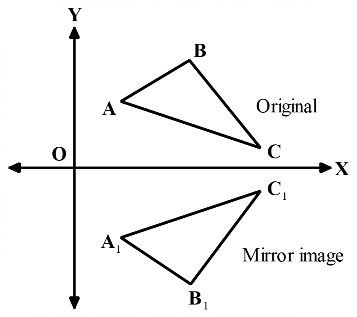
A. \[\left[ {\begin{array}{*{20}{c}} 0&1 \\ 1&0 \end{array}} \right]\]
B. \[\left[ {\begin{array}{*{20}{c}} 0&1 \\ { - 1}&0 \end{array}} \right]\]
C. \[\left[ {\begin{array}{*{20}{c}} { - 1}&0 \\ 0&1 \end{array}} \right]\]
D. \[\left[ {\begin{array}{*{20}{c}} 1&0 \\ 0&{ - 1} \end{array}} \right]\]
Answer: Option D
This Question Belongs to Engineering Maths >> Linear Algebra
Related Questions on Linear Algebra
A. 3, 3 + 5j, 6 - j
B. -6 + 5j, 3 + j, 3 - j
C. 3 + j, 3 - j, 5 + j
D. 3, -1 + 3j, -1 - 3j
A. 1024 and -1024
B. 1024√2 and -1024√2
C. 4√2 and -4√2
D. 512√2 and -512√2
Join The Discussion