The function x(t) is shown in the figure. Even and odd parts of a unit-step function u(t) are respectively,
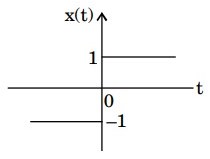
A. $$\frac{1}{2},\frac{1}{2}x\left( t \right)$$
B. $$ - \frac{1}{2},\frac{1}{2}x\left( t \right)$$
C. $$\frac{1}{2}, - \frac{1}{2}x\left( t \right)$$
D. $$ - \frac{1}{2}, - \frac{1}{2}x\left( t \right)$$
Answer: Option A
Related Questions on Signal Processing
The Fourier transform of a real valued time signal has
A. Odd symmetry
B. Even symmetry
C. Conjugate symmetry
D. No symmetry
A. $$V$$
B. $${{{T_1} - {T_2}} \over T}V$$
C. $${V \over {\sqrt 2 }}$$
D. $${{{T_1}} \over {{T_2}}}V$$
A. $$T = \sqrt 2 {T_s}$$
B. T = 1.2Ts
C. Always
D. Never
A. $${{\alpha - \beta } \over {\alpha + \beta }}$$
B. $${{\alpha \beta } \over {\alpha + \beta }}$$
C. α
D. β

Join The Discussion