The lagrangian of a particle of mass m moving in one dimension is $$L = \exp \left[ {\left( {\alpha t} \right)\frac{{M{{\dot x}^2}}}{2} - k{x^2}} \right]$$ where, $$\alpha $$ and k are positive constants. The equation of motion of the particle is
A. $$\ddot x + \alpha \dot x = 0$$
B. $$\ddot x + \frac{k}{m}x = 0$$
C. $$\ddot x - \alpha \dot x + \frac{k}{m}x = 0$$
D. $$\ddot x + \alpha \dot x + \frac{k}{m}x = 0$$
Answer: Option D
Join The Discussion
Comments (1)
A. increases till mass falls into hole
B. decreases till mass falls into hole
C. remains constant
D. becomes zero at radius r1, where 0 < r1 < r0
A. $$\frac{c}{3}$$
B. $$\frac{{\sqrt 2 }}{3}c$$
C. $$\frac{c}{2}$$
D. $$\frac{{\sqrt 3 }}{2}c$$
The Hamiltonian corresponding to the Lagrangian $$L = a{{\dot x}^2} + b{{\dot y}^2} - kxy$$ is
A. $$\frac{{{p_x}^2}}{{2a}} + \frac{{{p_y}^2}}{{2b}} + kxy$$
B. $$\frac{{{p_x}^2}}{{4a}} + \frac{{{p_y}^2}}{{4b}} - kxy$$
C. $$\frac{{{p_x}^2}}{{4a}} + \frac{{{p_y}^2}}{{4b}} + kxy$$
D. $$\frac{{{p_x}^2 + {p_y}^2}}{{4ab}} + kxy$$
A. circular
B. elliptical
C. parabolic
D. hyperbolic

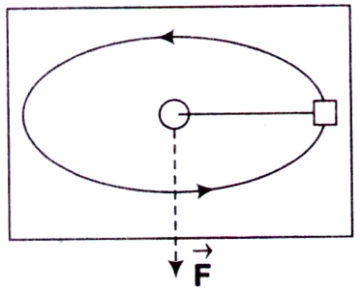
Explain the problem