Three pipes A, B and C can fill a tank in 6 hours, 9 hours and 12 hours respectively. B and C are opened for half an hour, then A is also opened. The time taken by the three pipes together to fill the remaining part of the tank is -
A. 3 hours
B. 2 hours
C. $${\text{2}}\frac{1}{2}$$ hours
D. $${\text{3}}\frac{1}{2}$$ hours
Answer: Option C
Solution (By Examveda Team)
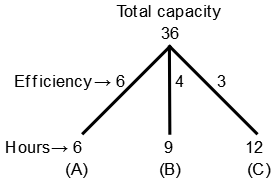
In half an hour (B + C) must have filled
$$ = \frac{4}{2} + \frac{3}{2} = \frac{7}{2}\,{\text{units}}$$
Capacity left
$${\text{ = 36}} - \frac{7}{2} = \frac{{65}}{2}\,{\text{units}}$$
Now all pipes will fill the remaining tank
$$\eqalign{ & {\text{ = }}\frac{{65}}{{2 \times \left( {6 + 4 + 3} \right)}} \cr & = \frac{{65}}{{2 \times 13}} \cr & = \frac{5}{2} \cr & = 2\frac{1}{2}\,{\text{hours}} \cr} $$
This Question Belongs to Arithmetic Ability >> Pipes And Cistern
LCM of 9, 9 and 12 is 36 ( 36 ltrs is the total capacity of the tank)
A= 36/6= 6ltrs /hour (so in 30min, 3ltrs of water A will filled in the tank)
B= 36/9 = 4ltrs/ hr ( in 30min 2ltrs)
&
C= 36/12= 3ltrs/hr ( in 30min 1.5 ltrs)
In 1st 30min B & C filled 3.5ltrs (2+1.5)
Then in another 30min A B & C together they filled 6.5(3+2+1.5) ltrs. ( That means in 1hour 10 ltrs of water is filled)
So remaining 26 ltrs of water( 36 - 10 )
:. The three pipe work together so they filled the tank in 1 hour is 13 ltrs
That's mean 13 + 10= 23 ltrs of water is filled in the tank in 2hours so in another 1hour 13ltrs of water again filled.
Now it is clear that in 3hours the tank is filled completely
May be wrong answer. Plz check. My finding is 3 hrs