When a body is subjected to biaxial stress i.e. direct stresses $$\left( {{\sigma _{\text{x}}}} \right)$$ and $$\left( {{\sigma _{\text{y}}}} \right)$$ in two mutually perpendicular planes accompanied by a simple shear stress $$\left( {{\tau _{{\text{xy}}}}} \right),$$ then minimum normal stress is
A. $$\frac{{{\sigma _{\text{x}}} + {\sigma _{\text{y}}}}}{2} + \frac{1}{2}\sqrt {{{\left( {{\sigma _{\text{x}}} - {\sigma _{\text{y}}}} \right)}^2} + 4\tau _{{\text{xy}}}^2} $$
B. $$\frac{{{\sigma _{\text{x}}} + {\sigma _{\text{y}}}}}{2} - \frac{1}{2}\sqrt {{{\left( {{\sigma _{\text{x}}} - {\sigma _{\text{y}}}} \right)}^2} + 4\tau _{{\text{xy}}}^2} $$
C. $$\frac{{{\sigma _{\text{x}}} - {\sigma _{\text{y}}}}}{2} + \frac{1}{2}\sqrt {{{\left( {{\sigma _{\text{x}}} + {\sigma _{\text{y}}}} \right)}^2} + 4\tau _{{\text{xy}}}^2} $$
D. $$\frac{{{\sigma _{\text{x}}} - {\sigma _{\text{y}}}}}{2} - \frac{1}{2}\sqrt {{{\left( {{\sigma _{\text{x}}} + {\sigma _{\text{y}}}} \right)}^2} + 4\tau _{{\text{xy}}}^2} $$
Answer: Option B
A. Equal to
B. Less than
C. Greater than
D. None of these
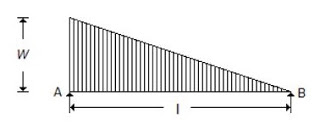
A. $$\frac{{{\text{w}}l}}{6}$$
B. $$\frac{{{\text{w}}l}}{3}$$
C. $${\text{w}}l$$
D. $$\frac{{2{\text{w}}l}}{3}$$
The columns whose slenderness ratio is less than 80, are known as
A. Short columns
B. Long columns
C. Weak columns
D. Medium columns

Join The Discussion