A man completes a certain journey by a car. If he covered 30% of the distance at the speed of 20kmph. 60% of the distance at 40km/h and the remaining of the distance at 10 kmph, his average speed is:

Solution (By Examveda Team)

$$\eqalign{ & {\text{Let the total distance be 100 km}}. \cr & {\text{Average speed}} \cr & = \frac{{{\text{total}}\,{\text{distance}}\,{\text{covered}}}}{{{\text{time}}\,{\text{taken}}}} \cr & = \frac{{100}}{{ { {\frac{{30}}{{20}}} + {\frac{{60}}{{40}}} + {\frac{{10}}{{10}}} } }} \cr & = \frac{{100}}{{ { {\frac{3}{2}} + {\frac{3}{2}} + 1 } }} \cr & = \frac{{100}}{{ {\frac{{ {3 + 3 + 2} }}{2}} }} \cr & = \frac{{ {100 \times 2} }}{8} \cr & = 25\,\text{kmph} \cr} $$

Alternate

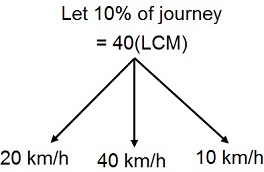
10% of journey's = 40 km
Then, total journey = 400 kms
$$\eqalign{ & {\text{And,}}\,{\text{Average speed}} \cr & = \frac{{{\text{Total distance }}}}{{{\text{Total time}}}} \cr & 30\% {\text{ of journey}} \cr & = 400 \times \frac{{30}}{{100}} \cr & = 120{\text{ km}} \cr & \cr & 60\% {\text{ of journey}} \cr & = 400 \times \frac{{60}}{{100}} \cr & = 240{\text{ km}} \cr & \cr & 10\% {\text{ of journey}} \cr & = 400 \times \frac{{10}}{{100}} \cr & = 40{\text{ km}} \cr & {\text{Average speed}} \cr & = \frac{{400}}{{\frac{{120}}{{20}} + \frac{{240}}{{40}} + \frac{{40}}{{10}}}} \cr & = \frac{{400}}{{ {6 + 6 + 4} }} \cr & = \frac{{400}}{{16}} \cr & \therefore {\text{Average speed}} = 25{\text{ km/hr}} \cr} $$