A man is watching from the top of a tower a boat speeding away from the tower. The boat makes an angle of depression of 45° with the man's eye when at a distance of 100 metres from the tower. After 10 seconds, the angle of depression becomes 30°. What is the approximate speed of the boat, assuming that it is running in still water?

Solution(By Examveda Team)

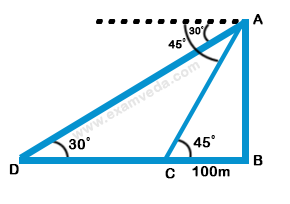
Consider the diagram shown above.
Let AB be the tower. Let C and D be the positions of the boat
Then, ∠ ACB = 45°, ∠ ADC = 30°, BC = 100 m
$$\eqalign{ & \tan {45^ \circ } = \frac{{AB}}{{BC}} \cr & \Rightarrow 1 = \frac{{AB}}{{100}} \cr & \Rightarrow AB = 100\,......\left( {eq:1} \right) \cr} $$
$$\tan {30^ \circ } = \frac{{AB}}{{BD}}$$
$$ \Rightarrow \frac{1}{{\sqrt 3 }} = \frac{{100}}{{BD}}$$     (∵ Substituted the value of AB from equation 1)
$$ \Rightarrow BD = 100\sqrt 3 $$
$$\eqalign{ & CD = \left( {BD - BC} \right) \cr & \,\,\,\,\,\,\,\,\,\,\, = \left( {100\sqrt 3 - 100} \right) \cr & \,\,\,\,\,\,\,\,\,\,\, = 100\left( {\sqrt 3 - 1} \right) \cr} $$
It is given that the distance CD is covered in 10 seconds.
i.e., the distance $$100\left( {\sqrt 3 - 1} \right)$$     is covered in 10 seconds.
$$\eqalign{ & {\text{Required}}\,{\text{speed}} \cr & = \frac{{{\text{Distance}}}}{{{\text{Time}}}} \cr & = \frac{{100\left( {\sqrt 3 - 1} \right)}}{{10}} \cr & = 10\left( {1.73 - 1} \right) \cr & = 7.3\,{\text{meter/seconds}} \cr & = 7.3 \times \frac{{18}}{5}\,{\text{km/hr}} \cr & = 26.28\,{\text{km/hr}} \cr} $$