Height And Distance - Aptitude MCQ Questions and Solutions with Explanations

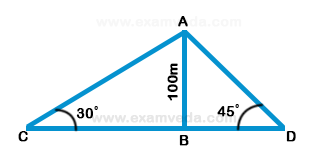
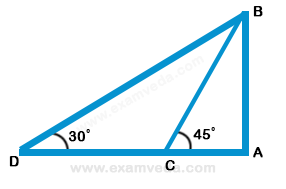
1

Two ships are sailing in the sea on the two sides of a lighthouse. The angle of elevation of the top of the lighthouse is observed from the ships are 30° and 45° respectively. If the lighthouse is 100 m high, the distance between the two ships is:

A) 173 m B) 200 m C) 273 m D) 300 m E) None of these

Discuss

Answer & Solution

Answer: Option C

Solution:

Let AB be the lighthouse and C and D be the positions of the ships.
Height and Distance mcq solution image

Then, AB = 100m, ∠ACB = 30° and ∠ADB = 45°
$$\frac{{AB}}{{AC}} = \tan {30^ \circ } = \frac{1}{{\sqrt 3 }}$$
$$ \Rightarrow AC = AB \times \sqrt 3 =100 \sqrt 3{\text{m}}$$
$$\frac{{AB}}{{AD}} = \tan {45^ \circ } = 1$$
$$ \Rightarrow AD = AB = 100{\text{m}}$$
∴ CD = (AC+AD) = (100√3 +100)
= 100(√3 +1) = 100(1.73+1) =100 × 2.73 = 273m

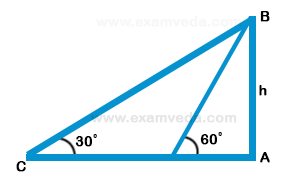
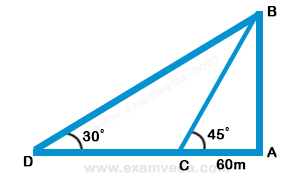
2

A man standing at a point P is watching the top of a tower, which makes an angle of elevation of 30º with the man's eye. The man walks some distance towards the tower to watch its top and the angle of the elevation becomes 60º. What is the distance between the base of the tower and the point P?

A) 4 √3 units B) 8 units C) 12 units D) Data inadequate E) None of these

Discuss

Answer & Solution

Answer: Option D

Solution:

One of AB, AD and CD must have given.
Height and Distance mcq solution image

So, the data is inadequate.

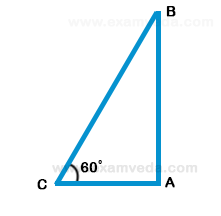
3

The angle of elevation of a ladder leaning against a wall is 60º and the foot of the ladder is 4.6 m away from the wall. The length of the ladder is:

A) 2.3 m B) 4.6 m C) 7.8 m D) 9.2 m

Discuss

Answer & Solution

Answer: Option D

Solution:

Let AB be the wall and BC be the ladder.
Height and Distance mcq solution image

Then, ∠ACB = 60° = AC = 4.6m
$$\frac{{AC}}{{BC}} = \cos {60^ \circ } = \frac{1}{2}$$
⇒ BC = 2 × AC = 2 × 4.6 = 9.2m

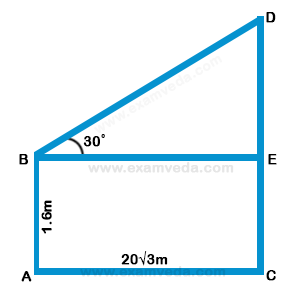
4

An observer 1.6 m tall is 20√3 away from a tower. The angle of elevation from his eye to the top of the tower is 30º. The heights of the tower is:

A) 21.6 m B) 23.2 m C) 24.72 m D) None of these

Discuss

Answer & Solution

Answer: Option A

Solution:

Let AB be the observer and CD be the tower.

Height and Distance mcq solution image

Draw BE ⊥ CD
Then CE = AB = 1.6m
BE = AC = 20√3m
$$\frac{{DE}}{{BE}} = \tan {30^ \circ } = \frac{1}{{\sqrt 3 }}$$
$$ \Rightarrow DE = \frac{{BE}}{{\sqrt 3 }} = \frac{{20\sqrt 3 }}{{\sqrt 3 }} = 20$$
∴ CD = CE + DE = (1.6 + 20) m = 21.6 m

5

From a point P on a level ground, the angle of elevation of the top tower is 30º. If the tower is 100 m high, the distance of point P from the foot of the tower is:

A) 149 m B) 156 m C) 173 m D) 200 m

Discuss

Answer & Solution

Answer: Option C

Solution:

Let AB be the tower.
Height and Distance mcq solution image

Then, ∠APB = 30° and AB = 100m
$$\frac{{AB}}{{AP}} = \tan {30^ \circ } = \frac{1}{{\sqrt 3 }}$$
⇒ AP = AB × √3 = 100 × √3
⇒ AP = 100 × 1.73 = 173m

6

The angle of elevation of the sun, when the length of the shadow of a tree √3 times the height of the tree, is:

A) 30º B) 45º C) 60º D) 90º

Discuss

Answer & Solution

Answer: Option A

Solution:

Let AB be the tree and AC be its shadow.
Height and Distance mcq solution image

Let ∠ACB = θ
$$\frac{{AC}}{{AB}} = \cot \theta $$
$$\frac{{AC}}{{AB}} = \sqrt 3 $$
$$\cot {30^ \circ } = \sqrt 3 $$
∴ θ = 30°

7

The angle of elevation of the top of a tower from a certain point is 30°. If the observed moves 20 m towards the tower, the angle of elevation the angle of elevation of top of the tower increases by 15°. The height of the tower is

A) 17.3 m B) 21.9 m C) 27.3 m D) 30 m

Discuss

Answer & Solution

Answer: Option C

Solution:

Let AB be the tower and C and D be the points of observation.
Then, ∠ACB = 30°, ∠ADB = 45° and CD = 20m
Let AB = h then,
$$\eqalign{ & \frac{{AB}}{{AC}} = \tan 30^\circ = \frac{1}{{\sqrt 3 }} \cr & \Rightarrow AC = AB \times \sqrt 3 = h\sqrt 3 {\kern 1pt} {\text{And,}} \cr & \Rightarrow \frac{{AB}}{{AD}} = \tan 45^\circ = 1 \cr & \Rightarrow AD = AB = h \cr & \, \, \, \, \, CD = 20 \cr & \Rightarrow \left( {AC - AD} \right) = 20 \cr & \Rightarrow h\sqrt 3 - h = 20 \cr & \therefore h = \frac{{20}}{{\left( {\sqrt 3 - 1} \right)}} \times \frac{{\left( {\sqrt 3 + 1} \right)}}{{\left( {\sqrt 3 + 1} \right)}} \cr & = 10\left( {\sqrt 3 + 1} \right){\text{m}} \cr & = \left( {10 \times 2.73} \right){\text{m}} \cr & = 27.3 {\text{m}} \cr} $$

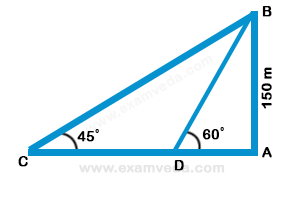
8

On the same side of tower, two objects are located. Observed from the top of the tower, their angles of depression are 45° and 60°. If the height of the tower is 150 m, the distance between the objects is-

A) 63.5 m B) 76.9 m C) 86.7 m D) 90 m

Discuss

Answer & Solution

Answer: Option A

Solution:

Let AB be the tower and C and D be the objects.
Then, AB = 150 m, ∠ACB = 45° and ∠ADB = 60°
$$\eqalign{ & \frac{{AB}}{{AD}} = \tan {60^ \circ } = \sqrt 3 \cr & \Rightarrow AD = \frac{{AB}}{{\sqrt 3 }} = \frac{{150}}{{\sqrt 3 }} \cr & \frac{{AB}}{{AC}} = \tan {45^ \circ } = 1 \cr & \Rightarrow AC = AB = 150{\text{ m}} \cr & \therefore CD = \left( {AC - AD} \right) \cr & = \left( {150 - \frac{{150}}{{\sqrt 3 }}} \right){\text{m}} \cr & = \left[ {\frac{{150\left( {\sqrt 3 - 1} \right)}}{{\sqrt 3 }} \times \frac{{\sqrt 3 }}{{\sqrt 3 }}} \right]{\text{m}} \cr & = 50\left( {3 - \sqrt 3 } \right){\text{m}} \cr & = \left( {50 \times 1.27} \right){\text{m}} \cr & = 63.5\,{\text{m}} \cr} $$

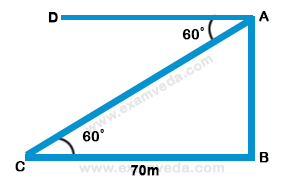
9

The angle of depression of a point situated at a distance of 70m from the base of a tower is 60°. The height of the tower is-

A) \[35\sqrt 3 {\text{ m}}\] B) \[70\sqrt 3 {\text{ m}}\] C) \[\frac{{70\sqrt 3 }}{3}{\text{ m}}\] D) \[{\text{70 m}}\]

Discuss

Answer & Solution

Answer: Option B

Solution:

Length of the tower AB = h meter.
$$\eqalign{ & \angle DAC = \angle ACB = {60^ \circ } \cr & BC = 70{\text{ meter}} \cr & {\text{In }}\vartriangle {\text{ABC,}} \cr & {\text{tan }}{60^ \circ } = \frac{{AB}}{{BC}} \cr & \Rightarrow \sqrt 3 = \frac{h}{{70}} \cr & \Rightarrow h = 70\sqrt 3 {\text{ meter}} \cr} $$

10

A man on the top of a vertical observation tower observes a car moving at a uniform speed coming directly towards it. If it takes 12 minutes for the angle of depression to change from 30° to 45°, how soon after this will the car reach the observation tower ?

A) 14 min. 35 sec. B) 15 min. 49 sec. C) 16 min. 23 sec. D) 18 min. 5 sec.

Discuss

Answer & Solution

Answer: Option C

Solution:

Let AB be the tower and C and D be the two positions of the car.
Then, \[\angle ACB = {45^ \circ },\] \[\angle ADB = {30^ \circ }\]
Let, AB = h, CD = x and AC = y
$$\eqalign{ & \frac{{AB}}{{AC}} = \tan {45^ \circ } = 1 \cr & \Rightarrow \frac{h}{y} = 1 \cr & \Rightarrow y = h \cr & \frac{{AB}}{{AD}} = \tan {30^ \circ } = \frac{1}{{\sqrt 3 }} \cr & \Rightarrow \frac{h}{{x + y}} = \frac{1}{{\sqrt 3 }} \cr & \Rightarrow x + y = \sqrt 3 h \cr & \therefore x = \left( {x + y - y} \right) \cr & \,\,\,\,\,\,\, = \sqrt 3 h - h \cr & \,\,\,\,\,\,\, = h\left( {\sqrt 3 - 1} \right) \cr} $$
Now, $$h\left( {\sqrt 3 - 1} \right)$$ is covered in 12 min.
So, h will be covered in→
$$\eqalign{ & \left[ {\frac{{12}}{{h\left( {\sqrt 3 - 1} \right)}} \times h} \right] \cr & = \frac{{12}}{{\left( {\sqrt 3 - 1} \right)}}\min \cr & = \left( {\frac{{1200}}{{73}}} \right)\min \cr & = 16\min ,\,\,23\sec \cr} $$