A man on the top of a vertical observation tower observers a car moving at a uniform speed coming directly towards it. If it takes 8 minutes for the angle of depression to change from 30° to 45°, how soon after this will the car reach the observation tower?

Solution(By Examveda Team)

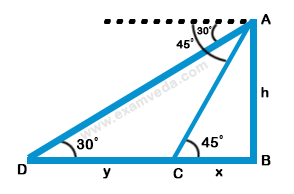
Consider the diagram shown above. Let AB be the tower. Let D and C be the positions of the car.
Then, ∠ ADC = 30° , ∠ ACB = 45°
Let AB = h, BC = x, CD = y
$$\eqalign{ & \tan {45^ \circ } = \frac{{AB}}{{BC}} = \frac{h}{x} \cr & \Rightarrow 1 = \frac{h}{x} \cr & \Rightarrow h = x\,......\left( 1 \right) \cr & \tan {30^ \circ } = \frac{{AB}}{{BD}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{{AB}}{{\left( {BC + CD} \right)}} \cr & \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \frac{h}{{x + y}} \cr & \Rightarrow \frac{1}{{\sqrt 3 }} = \frac{h}{{x + y}} \cr & \Rightarrow x + y = \sqrt 3 \,h \cr & \Rightarrow y = \sqrt 3 \,h - x \cr} $$
$$ \Rightarrow y = \sqrt 3 \,h - h$$     (∵ Substituted the value of x from equation 1 )
$$ \Rightarrow y = h\left( {\sqrt 3 - 1} \right)$$
Given that distance y is covered in 8 minutes.
i.e, distance $$h\left( {\sqrt 3 - 1} \right)$$   is covered in 8 minutes.
Time to travel distance x
= Time to travel distance h (∵ Since x = h as per equation 1).
Let distance h is covered in t minutes.
since distance is proportional to the time when the speed is constant, we have
$$\eqalign{ & h\left( {\sqrt 3 - 1} \right) \propto 8\,......\left( {\text{A}} \right) \cr & h \propto t\,..............\left( {\text{B}} \right) \cr & \frac{{\left( {\text{A}} \right)}}{{\left( {\text{B}} \right)}} \Rightarrow \frac{{h\left( {\sqrt 3 - 1} \right)}}{h} = \frac{8}{t} \cr & \Rightarrow \left( {\sqrt 3 - 1} \right) = \frac{8}{t} \cr & \Rightarrow t = \frac{8}{{\left( {\sqrt 3 - 1} \right)}} \cr & \,\,\,\,\,\,\,\,\,\,\, = \frac{8}{{\left( {1.73 - 1} \right)}} \cr & \,\,\,\,\,\,\,\,\,\,\, = \frac{8}{{.73}} \cr & \,\,\,\,\,\,\,\,\,\,\, = \frac{{800}}{{73}}\,{\text{minutes}} \cr & \,\,\,\,\,\,\,\,\,\,\, = 10\frac{{70}}{{73}}\,{\text{minutes}} \cr & \approx {\text{10}}\,{\text{minutes}}\,{\text{57}}\,{\text{seconds}} \cr} $$