A person, standing exactly midway between two towers, observes the top of the two towers at angle of elevation of 22.5° and 67.5°. What is the ratio of the height of the taller tower to the height of the shorter tower? (Given that tan 22.5° = $$\sqrt 2 - 1$$ )

Solution(By Examveda Team)

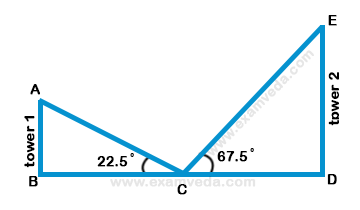
Let ED be the taller tower and AB be the shorter tower.
Let C be the point of observation
Given that ∠ ACB = 22.5° and ∠ DCE = 67.5°
Given that C is the midpoint of BD
Hence, BC = CD
$$\eqalign{ & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta \,ABC, \cr & \tan{22.5^ \circ } = \frac{{AB}}{{BC}}\,.....\left( {eq:1} \right)\, \cr & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta \,CDE, \cr & \tan {67.5^ \circ } = \frac{{ED}}{{CD}}\,.....\left( {eq:2} \right) \cr & \frac{{\left( {eq:2} \right)}}{{\left( {eq:1} \right)}} \Rightarrow \frac{{\tan {{67.5}^ \circ }}}{{\tan{{22.5}^ \circ }}} = \frac{{\left( {\frac{{ED}}{{CD}}} \right)}}{{\left( {\frac{{AB}}{{BC}}\,} \right)}} \cr & = \frac{{ED}}{{AB}}\,\,\,\,\,\left( {\because CD = BC} \right) \cr & \Rightarrow \frac{{\tan \left( {{{90}^ \circ } - {{22.5}^ \circ }} \right)}}{{\tan {{22.5}^ \circ }}} = \frac{{ED}}{{AB}} \cr & \Rightarrow \frac{{\cot {{22.5}^ \circ }}}{{\tan {{22.5}^ \circ }}} = \frac{{ED}}{{AB}} \cr & \,\,\,\,\,\,\,\,\,\,\left[ {\because \tan \left( {90 - \theta } \right) = \cot \theta } \right] \cr & \Rightarrow \frac{{\left( {\frac{1}{{\tan {{22.5}^ \circ }}}} \right)}}{{\tan {{22.5}^ \circ }}} = \frac{{ED}}{{AB}} \cr & \,\,\,\,\,\,\,\,\,\,\,\left[ {\because \cot \theta = \frac{1}{{\tan \theta }}} \right] \cr & \Rightarrow \frac{{ED}}{{AB}} = \frac{1}{{{{\left( {\tan {{22.5}^ \circ }} \right)}^2}}} \cr & = \frac{1}{{{{\left( {\sqrt 2 - 1} \right)}^2}}} \cr & = {\left( {\frac{1}{{\sqrt 2 - 1}}} \right)^2} \cr & = {\left[ {\frac{{\left( {\sqrt 2 + 1} \right)}}{{\left( {\sqrt 2 - 1} \right)\left( {\sqrt 2 + 1} \right)}}} \right]^2} \cr & = {\left[ {\frac{{\left( {\sqrt 2 + 1} \right)}}{{\left( {2 - 1} \right)}}} \right]^2} \cr & = {\left[ {\frac{{\left( {\sqrt 2 + 1} \right)}}{1}} \right]^2} \cr & = {\left( {\sqrt 2 + 1} \right)^2} \cr & = \left( {2 + 2\sqrt 2 + 1} \right) \cr & = \left( {3 + 2\sqrt 2 } \right) \cr & {\text{Required}}\,{\text{Ratio}} \cr & = ED:AB \cr & = \left( {3 + 2\sqrt 2 } \right):1 \cr} $$