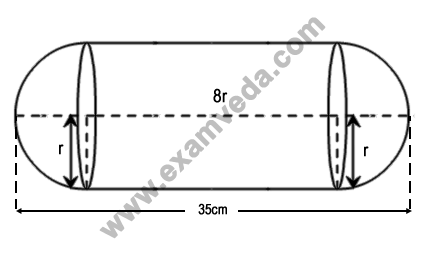
A solid is in the form of a right circular cylinder with hemispherical ends. The total length of the solid is 35 cm. The diameter of the cylinder is $$\frac{1}{4}$$ of its height. The surface area of the solid is :

Solution(By Examveda Team)

Let the radius of the cylinder and the hemisphere be r cm
Diameter of the cylinder = (2r) cm
Height of the cylinder = (4 × 2r) cm = 8r cm
Total length of the solid :
= (8r + r + r) cm = 10r cm
⇒ 10r = 35
⇒ r = 3.5

∴ Surface area of the solid :
= Curved surface area of the cylinder + 2 × (Curved surface area of the hemisphere)
$$ = \left( {2 \times \frac{{22}}{7} \times 3.5 \times 28 + 2 \times 2 \times \frac{{22}}{7} \times 3.5 \times 3.5} \right){\text{ c}}{{\text{m}}^2}$$
$$\eqalign{ & = \left( {616 + 154} \right){\text{ c}}{{\text{m}}^2} \cr & = 770{\text{ c}}{{\text{m}}^2} \cr} $$