A vertical pole fixed to the ground is divided in the ratio 1 : 9 by a mark on it with lower part shorter than the upper part. If the two parts subtend equal angles at a place on the ground, 15 m away from the base of the pole, what is the height of the pole?

Solution(By Examveda Team)

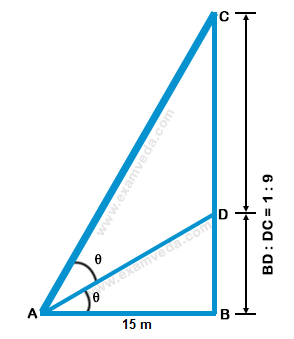
Let CB be the pole and point D divides it such that BD : DC = 1 : 9
Given that AB = 15 m
Let the the two parts subtend equal angles at point A such that ∠ CAD = ∠ BAD = $$\theta $$
From "Angle Bisector Theorem", we have
$$\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}}$$
$$ \Rightarrow \frac{1}{9} = \frac{{15}}{{AC}}$$     [∵ BD : DC = 1 : 9 and AB = 15(given)]
$$ \Rightarrow AC = 15 \times 9\,{\text{m}}\,......\left( {eq:1} \right)$$
$${\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta ABC,$$
$$CB = \sqrt {A{C^2} - A{B^2}} $$     (∵ Pythagorean theorem)
$$ = \sqrt {{{\left( {15 \times 9} \right)}^2} - {{15}^2}} $$     [∵AC=15 × 9(eq : 1) and AB=15 m(given)]
$$\eqalign{ & = \sqrt {{{15}^2} \times {9^2} - {{15}^2}} \cr & = \sqrt {{{15}^2}\left( {{9^2} - 1} \right)} \cr & = \sqrt {{{15}^2} \times 80} \cr & = \sqrt {{{15}^2} \times 16 \times 5} \cr & = 15 \times 4 \times \sqrt 5 \cr & = 60\sqrt 5 \,{\text{m}} \cr} $$