An aeroplane when 900 m high passes vertically above another aeroplane at an instant when their angles of elevation at same observing point are 60° and 45° respectively. Approximately, how many meters higher is the one than the other?

Solution(By Examveda Team)

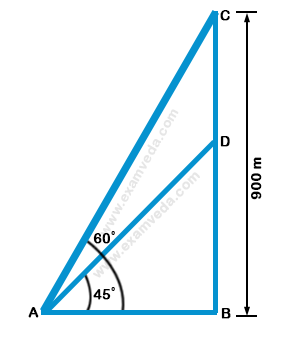
Let C and D be the position of the aeroplanes.
Given that CB = 900 m, ∠ CAB = 60°, ∠ DAB = 45°
$$\eqalign{ & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta ABC, \cr & \tan {60^ \circ } = \frac{{CB}}{{AB}} \cr & \sqrt 3 = \frac{{900}}{{AB}} \cr & AB = \frac{{900}}{{\sqrt 3 }} \cr & \,\,\,\,\,\,\,\,\,\, = \frac{{900 \times \sqrt 3 }}{{\sqrt 3 \times \sqrt 3 }} \cr & \,\,\,\,\,\,\,\,\,\, = \frac{{900\sqrt 3 }}{3} \cr & \,\,\,\,\,\,\,\,\,\, = 300\sqrt 3 \cr & {\text{From}}\,{\text{the}}\,{\text{right}}\,\Delta ABD, \cr & \tan {45^ \circ } = \frac{{DB}}{{AB}} \cr & 1 = \frac{{DB}}{{AB}} \cr & DB = AB = 300\sqrt 3 \cr & \cr & {\text{Required}}\,{\text{height}} \cr & = CD \cr & = \left( {CB - DB} \right) \cr & = \left( {900 - 300\sqrt 3 } \right) \cr & = \left( {900 - 300 \times 1.73} \right) \cr & = \left( {900 - 519} \right) \cr & = 381\,{\text{m}} \cr} $$