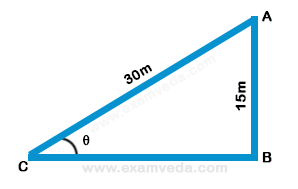
11. If a 30 m ladder is placed against a 15 m wall such that it just reaches the top of the wall, then the elevation of the wall is equal to-
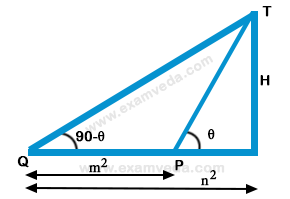
12. The angles of elevation of the top of from two points P and Q at distance $${{m^2}}$$ and $${{n^2}}$$ respectively, from the base and in the same straight line with it are complementary. The height of the tower is-
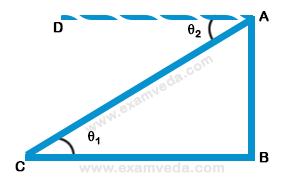
13. A boy is standing at the top of the tower and another boy is at the ground at some distance from the foot of the tower, then the angle of elevation and depression between the boys when both look at a each other will be-
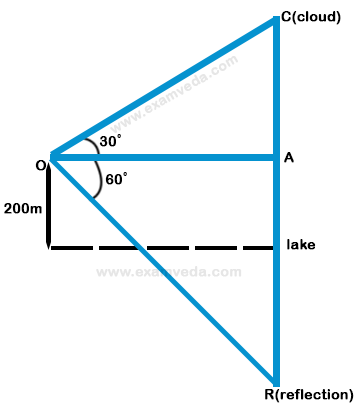
14. The angle of elevation of a cloud from a point 200 m above a lake is 30° and the angle of depression of its reflection in the lake is 60°. The height of the cloud is-
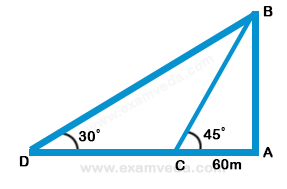
15. A man is watching from the top of tower a boat speeding away from the tower. The boat makes an angle of depression of 45° with the man’s eye when at a distance of 60 meters from the tower. After 5 seconds, the angle of depression becomes 30°. What is the approximate speed of the boat, assuming that it is running in still water?
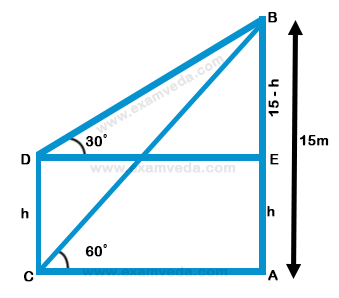
16. The top of a 15 metre high tower makes an angle of elevation of 60° with the bottom of an electric pole and angle of elevation of 30° with the top of the pole. What is the height of electric pole ?
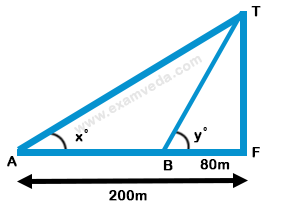
17. TF is a tower with F on the ground. The angle of elevation of T from A is x° such that tan x°= $$\frac{2}{5}$$ and AF = 200 m. The angle of elevation of T from a nearer point B is y° with BF = 80 m. The value of y° is-
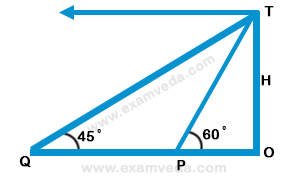
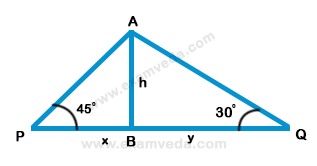
18. From the top of a tower, the angles of depression of two objects P and Q (situated on the ground on the same side of the tower) separated at a distance of 100$${\left( {3 - \sqrt 3 } \right)}$$ m are 45° and 60 ° respectively. The height of the tower is-
19. From a lighthouse the angles of depression of two ships on opposite sides of the light house are observed to be 30° and 45°. If the height of the lighthouse is h metres, the distance between the ships is
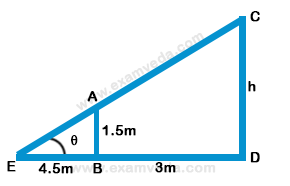
20. If a 1.5 m tall girl stands at a distance of 3 m from a lamp-post and casts a shadow of length 4.5 m on the ground, then the height of the lamp-post is
Read More Section(Height and Distance)
Each Section contains maximum 100 MCQs question on Height and Distance. To get more questions visit other sections.