Important Theory / Shots Trick on Triangles
Section 1
Section 2
61. An isosceles triangle ABC is right-angled at B. D is a point inside the triangle ABC. P and Q are the feet of the perpendiculars drawn from D on the side AB and AC respectively of ΔABC. If AP = a cm, AQ = b cm and ∠BAD = 15°, sin 75° = ?
62. In a triangle ABC, the side BC is extended up to D such that CD = AC. If ∠BAD = 109° and ∠ACB = 72° then the value of ∠ABC is
63. The equidistant point from the vertices of a triangle is called its:
64. Let ABC be an equilateral triangle and AX, BY, CZ be the altitudes. Then the right statement out of the four given responses is
65. ABC is an isosceles triangle with AB = AC. The side BA is produced to D such that AB = AD. If ∠ABC = 30°, then ∠BCD is equal to
66. The sum of three altitudes of a triangle is
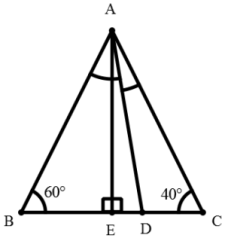
67. In ΔABC, ∠B = 60° and ∠C = 40°. If AD and AE be respectively the internal bisector of ∠A and perpendicular on BC, then the measure of ∠DAE is
68. In a right-angled triangle, the product of two sides is equal to half of the square of the third side i.e., hypotenuse. One of the acute angle must be
69. In a ΔABC ∠A : ∠B : ∠C = 2 : 3 : 4. A line CD drawn || to AB, then the ∠ACD is :
70. BL and CM are medians of ΔABC right-angled at A and BC = 5 cm. If BL = $$\frac{{3\sqrt 5 }}{2}$$ cm, then the length of CM is
Read More Section(Triangles)
Each Section contains maximum 100 MCQs question on Triangles. To get more questions visit other sections.