Important Theory / Shots Trick on Triangles
Section 1
Section 2
1. Given that the ratio of altitudes of two triangles is 4 : 5, ratio of their areas is 3 : 2, the ratio of their corresponding bases is :
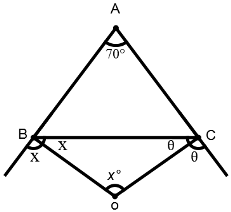
2. In ΔABC, the external bisectors of the angles ∠B and ∠C meet at the point O. If ∠A = 70°, then the measure of ∠BOC is :
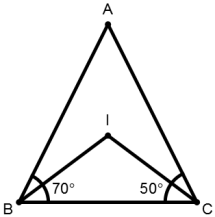
3. If I be the incentre of ΔABC and ∠B = 70° and ∠C = 50°, then the magnitude of ∠BIC is
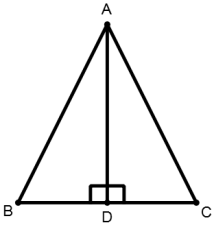
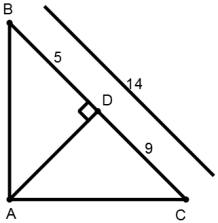
4. In ΔABC, if AD ⊥ BC, then AB2 + CD2 is equal to
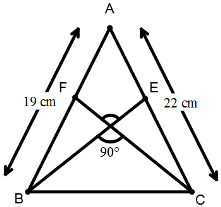
5. If in a triangle ABC, BE and CF are two medians perpendicular to each other and if AB = 19 cm and AC = 22 cm then the length of BC is :
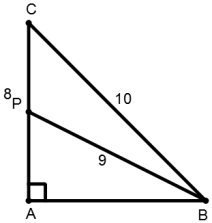
6. ABC is a triangle in which ∠A = 90°. Let P be any point on side AC. If BC = 10 cm, AC = 8 cm and BP = 9 cm, then AP = ?
7. ∠A of ΔABC is a right angle. AD is perpendicular on BC. If BC = 14 and BD = 5 cm, then measure of AD is:
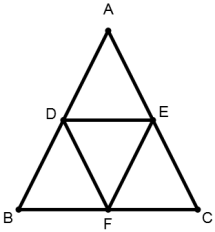
8. For a triangle ABC, D, E, F are the mid - point of its sides. If ΔABC = 24 sq. units then ΔDEF is :
9. ∠A + $$\frac{1}{2}$$ ∠B + ∠C = 140°, then ∠B is :
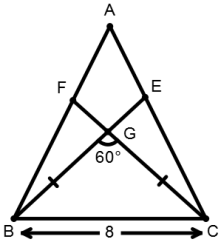
10. If two medians BE and CF of a triangle ABC, intersect each other at G and if BG = CG, ∠BGC = 60°, BC = 8 cm, then area of the triangle ABC is:
Read More Section(Triangles)
Each Section contains maximum 100 MCQs question on Triangles. To get more questions visit other sections.